Encontre o valor médio de em .
Passo 1
Por definição o valor médio de uma função em um certo intervalo é dado por:
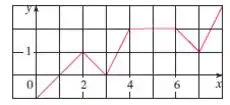
Contudo como temos o desenho da função, podemos primeiro dividir nosso intervalo de em vários pequenos intervalos nos quais podemos visualizar o valor de no gráfico para cada subintervalo e depois disso calculamos o valor médio. Assim, temos que:
Passo 2
Por fim, o valor médio pode ser calculado como: