Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.9 - Ex. 35a
35.
(a) Mostre que (a função de Bessel de ordem 0 dada no Exemplo 4) satisfaz a equação diferencial
Passo 1
E aê, gente bonita!
Questão trabalhosa essa aí! FORÇA NA PERUCA!
A questão quer que você olhe no seu livro a função de Bessel no Exemplo 4 do livro
e pergunta se ela satisfaz a equação diferencial
Moleza! Respira e não pira.
A primeira coisa a se fazer é calcular a primeira e a segunda derivadas da função de Bessel, que são essas aqui:
Passo 2
Agora vamos substituir a função de Bessel e suas derivadas, na forma de série, na equação diferencial dada no exercício:
Passando as variáveis de pra dentro dos somatórios obtemos:
Nota-se que o terceiro somatório, originado de , começa em , diferentemente dos outros dois, que começam de .
Vamos modificar esse somatório de forma que seu índice também se inicie em .
Para fazer isso sem alterar os termos da série, basta substituir por dentro do termo geral da mesma. Tranquilo, né?!
Assim temos:
Passo 3
No ponto em que estamos é possível ver que os termos gerais das séries acima são muito semelhantes. Contudo, ainda é possível melhorar a termo geral da terceira série de forma que ela fique mais parecida com as outras duas. Por isso vamos fazer uma manipulação algébrica e simplificação para ajustá-la.
Abrimos um parênteses na resolução geral do exercício para que você entenda a manipulação feita na série citada. MUITA ATENÇÃO no passo a passo!
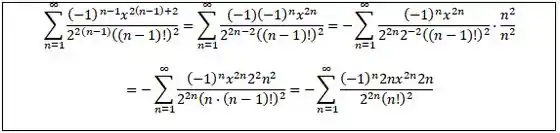
Passo 4
Voltando à resolução geral, já com a terceira série ajustada, temos:
Agora, FINALMENTE, podemos colocar em evidência os vários termos que as séries têm em comum.
Resposta
A função de Bessel satisfaz a equação diferencial.