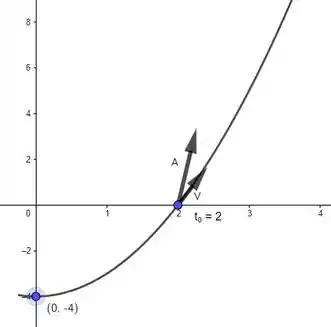
Um objeto inicia seu movimento no ponto , e se move ao longo da parábola , com velocidade horizontal . Encontre o vetor posição do objeto, os vetores velocidade e aceleração no instante e represente-os geometricamente.
Passo 1
Pra começar, bora olhar pra velocidade horizontal:
Galera, se dermos uma mexidinha nisso, conseguimos escrever uma expressão pra ! Quer ver?
Como o objeto inicia seu movimento no ponto , então, pra , a posição será:
Passo 2
Beleza, agora se usarmos a parametrização pro vetor posição:
Sabendo que:
Vamos ter o seguinte resultado:
E seja os vetores velocidade e aceleração:
Derivando, chegamos em:
No intante , como o enunciado pediu, chegamos ao fim da questão!
Esboçando:
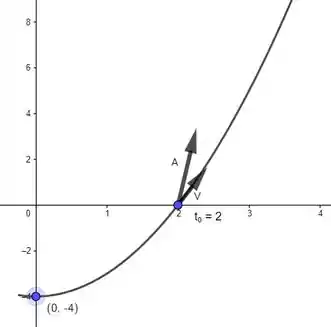
Resposta