Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.4 - Ex. 34
Um objeto com peso é arrastado ao longo de um plano horizontal por uma força agindo ao longo de uma corda atada ao objeto. Se a corda faz um ângulo com o plano, então a grandeza da força é
Onde é uma constante chamada coeficiente de atrito
- Encontre a taxa de variação de em relação a
- Quando essa taxa de variação é igual a 0?
- Se e , faça o gráfico de como uma função de e use-o para localizar o valor de para o qual . Esse valor é consistente com a resposta dada na parte (b)
Passo 1
Opa, bora lá!
a) Inicialmente, ele nos pede para encontrarmos a derivada de em relação a . Então vamos lá!
Usando a regra do quociente, temos:
Como é uma constante, temos:
Logo,
Passo 2
b) Agora vamos ver quando essa derivada será zero. Vem comigo!
Então,
Agora basta fazermos o numerador igual a zero. Como :
Assim,
Então
,
Portanto, a derivada será nula quando
Passo 3
c) Se e :
Fazendo um gráfico para a situação que ele nos descreve:
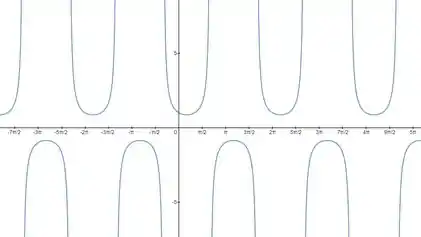
Pelo gráfico, vemos que os ponto onde :
Do item (b):
Para :
Para :
O que verifica que o valor é consistente.
Prontinho!
Resposta
,