Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.6 - Ex. 12
Obtenha os gráficos de que revelem todos os aspectos importantes da curva. Estime os intervalos de crescimento e decrescimento, valores extremos, intervalos de concaviade e pontos de inflexão, e use o cálculo para achar essas quantidades exatamente.
Passo 1
Vamos começar fazendo o gráfico dessa função no intervalo que foi dado. Não precisa ser nada muito preciso, só queremos fazer algumas estimativas!
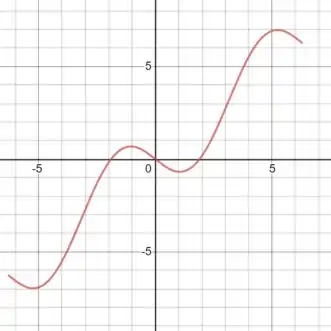
Vamos começar procurando os intervalos de crescimento e decrescimento.
Olhando para o gráfico, e considerando que cada quadrado no eixo vale uma unidade, podemos estimar que a função é crescente nos seguintes intervalos:
E é decrescente em:
Passo 2
Agora vamos procurar valores extremos. A função tem máximos em:
E tem mínimos em:
Passo 3
As concavidades podem ser um pouco mais difíceis de enxergar, então vamos marcar no desenho:
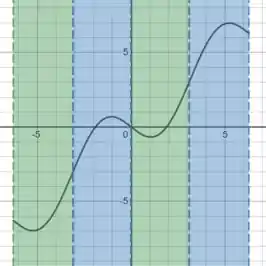
Os trechos em azul representam convavidades para baixo:
E os trechos em verde representam concavidades para cima:
E os pontos de inflexão estão justamente nos limites desses intervalos:
Passo 4
Beleza, agora vamos procurar esses mesmos elementos de forma exata, usando cálculo.
Para encontrar os intervalos de crescimento, precisamos da derivada primeira da função:
Enquanto essa derivada for positiva, a função é crescente. Enquanto ela for negativa, a função é decrescente. Vamos encontrar cada um desses intervalos, começando pela parte crescente da função:
E já que estamos limitados em
E a parte decrescente é o intervalo restante:
Passo 5
Para encontrar os valores extremos, usamos o teste da primeira derivada:
No nosso caso:
E essa função é satisfeita por quatro pontos. Os pontos de máximo estão em:
E os pontos de mínimo estão em:
Se não tivéssemos o gráfico, como faríamos para saber quais desses pontos extremos são de mínimo e de máximo?
Teríamos que olhar para as concavidades, vamos fazer isso agora.
Passo 6
Para determinar as concavidades, precisamos da derivada segunda da função:
Quando essa função é positiva, a curvatura é para cima, isso acontece em:
Nesse intervalo, todos os pontos extremos são de mínimo.
Quando essa função é negativa, a curvatura é para baixo, isso acontece em:
Nesse intervalo, todos os pontos extremos são de máximo.
Os pontos de inflexão acontece quando a função passa de um intervalo positivo para um negativo, então os pontos de inflexão estão em:
Resposta
A função é crescente em e decrescente em . A função tem pontos de máximo em e , e pontos de mínimo em e . A concavidade é parra cima em e para baixo em . Os pontos de inflexão estão em .