Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 7

Avalie a integral dada mudando para coordenadas polares.

∬ D x 2 y   d A ,   onde D é a metade superior do disco com centro na origem e raio 5 .

Passo 1

Faaaala turminha fera!!! Tudo bem?

Vamos avaliar a questão. Precisamos resolver a integral dupla dada:

∬ D x 2 y   d A

Onde D é a metade superior do disco com centro na origem e possui raio igual a 5 .

Tá, mas e agora? Como resolvo?

Bom, a gente quer passar isso pra coordenadas polares, certo?! Belê, vamos lembrar que:

x = r cos ⁡ θ

y = r sen ⁡ θ

d A = r d r d θ

Até aqui ok! Vamos pensar na nossa região D . Sabemos que o raio varia de 0 até 5 . Já o ângulo, repare bem no que ele falou no enunciado...que D é a metade superior do disco centrado na origem...logo concluímos que nosso ângulo varia entre 0 e π .

Fazer um esboço da região sempre ajuda a compreender, compare a imagem abaixo com o que falamos acima.

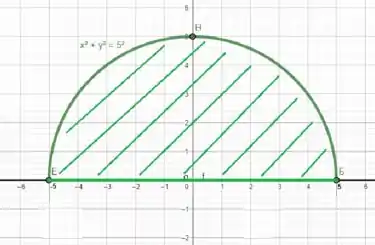
Então, temos:

D = r , θ 0 ≤ r ≤ 5 ,   0 ≤ θ ≤ π }

Agora, vamos colocar mão na massa pessoal! Partiu!!!

Passo 2

Vamos começar relembrando nossa equação:

∬ D x 2 y   d A =

Em coordenadas polares temos:

x = r cos ⁡ θ

y = r sen ⁡ θ

d A = r d r d θ

Logo, nossa integral fica

∬ D [ r cos ⁡ θ ) 2 r sen ⁡ θ   r   d r   d θ

∬ D r 4 cos 2 ⁡ θ sen ⁡ θ d r   d θ

Agora vamos com calma. Precisamos escrever ainda os limites de integração da região D . Vamos esboçar o que ele menciona no enunciado.

Compare a imagem abaixo com o que é dito: D é a metade superior do disco com centro na origem e raio 5 .

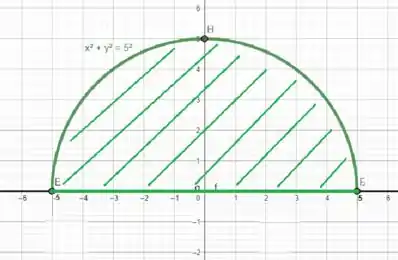
Veja como fica mais fácil extrair nossa região D quando esboçamos.

Logo, D é:

D = r , θ 0 ≤ r ≤ 5 ,   0 ≤ θ ≤ π }

Show, então já sabemos os limites de integração!

Agora que temos nossos limites de integração, vamos resolver nossa integral!!!

Passo 3

Colocando os limites de integração, vamos ter a seguinte integral:

∫ 0 π ∫ 0 5 r 4 cos 2 ⁡ θ sen ⁡ θ   d r   d θ

Vamos começar integrando de dentro para fora, ou seja, primeiro em d r :

∫ 0 π cos 2 ⁡ θ sen ⁡ θ   ∫ 0 5 r 4 d r d θ

Integrando:

∫ 0 π cos 2 ⁡ θ sen ⁡ θ   r 5 5 0 5   d θ

Aplicando os limites de integração, vamos ter:

∫ 0 π cos 2 ⁡ θ sen ⁡ θ   5 5 5 d θ

∫ 0 π 625 cos 2 ⁡ θ sen ⁡ θ     d θ

Agora vamos pegar esse resultado e aplicar na integral de fora!

Passo 4

Temos a seguinte integral para resolver:

625 ∫ 0 π cos 2 ⁡ θ sen ⁡ θ d θ

Vamos fazer uma substituição simples

u = cos ⁡ θ

d u = - sen ⁡ θ d θ

Logo,

625 ∫ - u 2 d u = - 625 u 3 3

Voltando pra função cos ⁡ θ , teremos:

- 625 cos 3 ⁡ θ 3 0 π

Aplicando os limites vamos ter:

- 625 * ( cos 3 ⁡ π - cos 3 ⁡ 0 ) 3 = 1250 3

Logo, a resposta da nossa integral é:

∬ D x 2 y   d A = 1250 3

Resposta

∬ D x 2 y   d A = 1250 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 1-8, descreva a região dada em coordenadas polares.
Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ 0 2 ∫ 0 x yd yd x
Nos Exercícios 1-8, descreva a região dada em coordenadas polares. A região delimitada pela semicircunferência x 2 + y 2 = 2 y ,y ≥ 0
Nos Exercícios 1-8, descreva a região dada em coordenadas polares.
Nos Exercícios 1-8, descreva a região dada em coordenadas polares.