Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 4.3 - Ex. 7

Uma partícula desloca-se sobre o eixo 0 x com aceleração constante a , a > 0 . Suponha que no instante t = 0 a velocidade seja zero. A velocidade no instante t é, então, dada por v t = a t .

Divida o intervalor de tempo 0 , T em n intervalos de amplitudes iguais a T n :

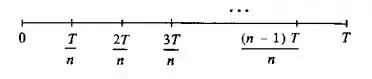
No instante T n a velocidade será a T n , no instante 2 T n , será 2 a T n etc. Supondo n suficientemente grande, o espaço percorrido entre os instantes T n e 2 T n será aproximadamente a T n ∙ T n (por quê?); entre os instantes 2 T n e 2 T n o espaço percorrido será aproximadamente 2 a T n ∙ T n etc.

a) Calcule lim n → + ∞ ⁡ a T n ∙ T n + 2 a T n ∙ T n + … + n - 1 a T n ∙ T n

b) Interprete cinematicamente e geometricamente o limite acima.

Passo 1

a) Podemos escrever a soma como:

a T n ∙ T n + 2 a T n ∙ T n + … + n - 1 a T n ∙ T n = a T 2 n 2 1 + 2 + 3 + … + n - 1 = a T 2 2 1 - 1 n

Assim:

lim n → + ∞ ⁡ a T n ∙ T n + 2 a T n ∙ T n + … + n - 1 a T n ∙ T n = lim n → + ∞ ⁡ a T 2 2 1 - 1 n = a T 2 2 1 - 0

Logo:

lim n → + ∞ ⁡ a T n ∙ T n + 2 a T n ∙ T n + … + n - 1 a T n ∙ T n = a T 2 2

Passo 2

b) Cinematicamente, o limite que calculamos no item (a) nos dá justamente o espaço percorrido pela partícula entre os instantes t = 0 e t = T .

Resposta

lim n → + ∞ ⁡ a T n ∙ T n + 2 a T n ∙ T n + … + n - 1 a T n ∙ T n = a T 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o gráfico da sequência para decidir quando a sequência é convergente ou divergente. Se a sequênca é convergente, estime o valor do limite a partir do gráfico e, então, prove seu palpite. (Veja na
Determine se a sequência converge ou diverge. Se convergir, encontre o limite. a n = n ! 2 n
Use o gráfico da sequência para decidir quando a sequência é convergente ou divergente. Se a sequência é convergente, estime o valor do limite a partir do gráfico e, então, prove seu palpite. (Veja na
Determine se a sequência converge ou diverge. Se convergir, encontre o limite. a n = - 3 n n !
Use o gráfico da sequência para decidir quando a sequência é convergente ou divergente. Se a sequência é convergente, estime o valor do limite a partir do gráfico e, então, prove seu palpite. (Veja na