Uma partícula move-se segundo a lei do movimento , , onde é medido em segundos e , em pés.
(a) Encontre a velocidade no instante .
(b) Qual a velocidade depois de ?
(c) Quando a partícula está em repouso?
(d) Quando a partícula está se movendo no sentido positivo?
(e) Encontre a distância total percorrida durante os 8 primeiros segundos.
(f) Desenhe um diagrama como na Figura 2 para ilustrar o movimento da partícula.
Passo 1
Fala aí. Tudo belezinha por aí?
Bom, essa questão deu pra gente a função
Dizendo que uma partícula se move segundo a lei do movimento , , onde é medido em segundos e em pés.
E pede pra gente analisar essa função e responder as seguintes perguntas:
a) Encontre a velocidade no instante .
b) Qual a velocidade depois de s?
c) Quando a partícula está em repouso?
d) Quando a partícula está se movendo no sentido positivo?
e) Encontre a distância total percorrida durante os primeiros segundos.
f) Desenhe um diagrama como na figura para ilustrar o movimento da partícula.
Eita! Bastante coisa, né? Mas calma. Vamos relembrar algumas coisas importantes aqui:
Quando temos a função que determina a velocidade de uma partícula com o passar do tempo, podemos encontrar a função velocidade derivando a função posição. Isso vai ajudar a gente a resolver todos os itens.
Vamos ver cada um deles no passo a passo. Bora!
Passo 2
Precisamos, no item a) encontrar a velocidade no instante .
Lembrando que derivada da função posição, é a velocidade, teremos:
Prontinho. Agora vamos usar essa função velocidade para responder aos outros itens.
Passo 3
No item b) vamos calcular a velocidade depois de s.
Para isso apenas precisamos substituir , e calcular. Veja:
Show. Próxima!
Passo 4
Nesse passo, devemos responder, c) Quando a partícula está em repouso.
(c)
A partícula vai estar em repouso quando .
Assim, basta igualar a função velocidade a zero e resolver a equação. Veja:
Colocando o em evidência:
E fatorando o como uma diferença de cubos, teremos:
Encontrando as raízes de cada fator teremos como única opção real:
Essa foi!
Passo 5
Agora vamos dizer no item d) quando a partícula está se movendo no sentido positivo.
A partícula está se movendo no sentido positivo quando .
E agora o que era uma equação, se torna uma inequação. Veja:
Portanto, pelo resultado da letra (c), .
Passo 6
E para saber a distância total percorrida durante os primeiros segundos e responder ao item e), basta lembrar que a distância total é dada pela diferença entre os valores até chegar em , vamos lá:
Somando esses valores temos que a distância total é .
Passo 7
E finalmente no item f) O diagrama que representa esse movimento da partícula é:
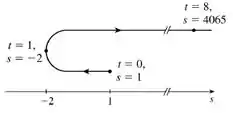
Prontinho!!
Resposta
(a);
(b);
(c) ;
(d) ;
(e) a distância total é.;
(f) diagrama.