Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 23
Um recipiente com a forma de um paralelepípedo com base quadrada deve ter um volume de . O custo da base e da tampa é o dobro do custo dos lados. Encontre as dimensões do recipiente de menor custo.
Passo 1
Vamos escrever a expressão para o volume do paralelepípedo, considerando o lado da base quadrada como e a altura como . Temos:
Vamos agora determinar uma expressão para o custo de confecção do paralelepípedo.
Vamos pensar: precisamos de uma base, uma tampa (que são exatamente iguais) e as 4 laterais, todas iguais entre si. Uma ilustração pode ajudar:
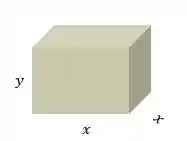
A base e a tampa, que são iguais, tem áreas equivalentes a . Como é uma base e uma tampa, temos o custo duplicado, que será:
onde é o custo do centímetro quadrado do material.
Os 4 lados, que são retangulares, de área , vão ter um custo que é a metade do custo da base (e da tampa):
A expressão pro custo total do paralelepípedo pode ser escrita pela soma dessas expressões, que vai ser:
Passo 2
Temos uma expressão pro custo que depende de duas variáveis, e . Podemos fazer ela depender só de uma, como , pela expressão do volume . Isolamos e temos:
Agora, substituímos essa sentença na expressão do custo, pra termos um :
Passo 3
Como precisamos determinar o menor custo possível e já temos uma função pro custo, vamos derivá-la, igualar a derivada a zero e determinar assim os pontos críticos, que são pontos de máximo ou de mínimo da função.
No caso, nos interessa o ponto de mínimo. O valor de associado ao ponto de mínimo vai equivaler ao comprimento da base (e da tampa) do paralelepípedo de menor custo possível.
Derivando, (lembrando que , o custo, é uma constante) temos:
Igualamos a zero:
Tiramos as raízes cúbicas de ambos os lados:
Passo 4
Determinamos . Agora precisamos de , que obtemos facilmente pela expressão que já temos:
Resposta
São as dimensões e .