Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 42

42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método.

x = y - 3 2 ,   x = 4 ; em torno de y = 1 .

Passo 1

Faaala ae! Beleza??

Nesse problema temos que obter o volume do solido gerado pela revolução da area entre a equação x = y - 3 2 e x = 4 em torno de y = 1 .

Tem ideia de como fazemos isso? 👀

A região que será revolucionada é dada pela area entre x = y - 3 2 e x = 4 , ou seja:

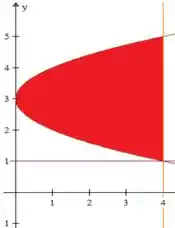
Se liga, nós temos a seguinte função de x :

y = ± x + 3

Então, temos uma parte da função para + x (parte mais acima) e outra para - x (parte mais abaixo). Você concorda comigo que teremos um volume para cada uma dessas partes?

O que acontece é que o se a gente subtrai o volume da parte de cima pelo da parte de baixo, teremos exatamente o volume que queremos!!

Então, a área pelo método dos anéis será:

A x = π f 1 x - 1 2 - π f 2 x - 1 2

Onde f 1 x = x + 3 e f 2 x = - x + 3 .

Veja só! 😬

Passo 2

O volume da figura rotacionada será:

V = ∫ 0 4 A x d x

V = ∫ 0 4 π f 1 x - 1 2 - π f 2 x - 1 2 d x

Agora, é só substituir as funções e resolver essa integral! Bora lá:

V = π ∫ 0 4 x + 3 - 1 2 - - x + 3 - 1 2 d x

V = π ∫ 0 4 x + 2 2 - - x + 2 2 d x

V = π ∫ 0 4 x + 4 x + 4 - x + 4 x - 4 d x

Simplificando...

V = π ∫ 0 4 8 x 1 2 d x

Calculando a integral e aplicando os limites de integração...

V = 8 π 2 3 x 3 2 0 4

V = 8 π 2 3 4 3 2 - 2 3 0 3 2

V = 8 π 2 3 8

V = 128 π 3

Prontinho! O que achou? Responde Aí! 😊

Resposta

V = 128 π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo x y = cos ⁡ x y = 0 x = 0 0 ≤ x ≤ π 2
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo x y = x - x 2 y = 0
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo x y = cotg ⁡ x e i x oxd ex = π 6ax = π 2
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo y x = y 3 2 x = 0 y = 2
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo y x = cos ⁡ π y 4 - 2 ≤ y ≤ 0 x = 0