Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.2 - Ex. 2

Seja F (x) = int_0^x f (t) d t onde f (t) = {_(2 s e t = 1)^(t s e t != 1)

  1. Esboce o gráfico de F
  2. Calcule F ' ( x )

Passo 1

a) Para esboçarmos o gráfico, precisamos integrar e ver qual o jeitão da função F ( x ) . Então vamos partir para integral!

F (x) = int_0^x f (t) d t

Passo 2

Integrando, temos:

F (x) = int_0^x t d t

Não esquece: int x^n d x = (x^(n + 1))/(n + 1) + c quando n != - 1

F (x) = (t^2)/(2) |_0^x

Fazendo as contas:

F (x) = (x^2)/(2) - (0^2)/(2) -> F (x) = (x^2)/(2)

Esboçando um gráfico:

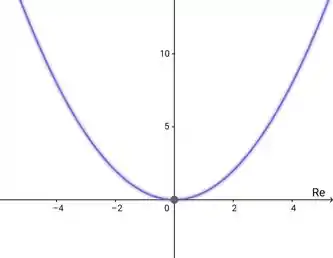
Passo 3

b) Como já achamos F ( x ) , basta derivar. Assim,

F (x) = (x^2)/(2)

Derivando,

F^' (x) = 2 xx (x^(2 - 1))/(2)

Logo,

F^' (x) = x

Resposta

F^' (x) = x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja F(x) = ∫ 0 x f t d to n d ef t ={ 2 s e t=1 1 s e t≠1 Verifique que F'(x) = f(x) em todo x em que f for contínua.F é derivável em x = 1? Em caso afirmativo, calcule F'(1) e compare com f(1).
Esboce o gráfico da função F dada pore) F x = ∫ 0 x f t d t onde f t = ts e - 2 ≤ t ≤ 0 e - ts e t0
Esboce o gráfico da função F dada pora) F x = ∫ 0 x f t d t onde f t = 2s e 0 ≤ t1 1 t s et ≥ 1
Esboce o gráfico da função F dada porc) F x = ∫ 1 x f t d t ondef t =2s et ≤ 0 0s et0