Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 8
Seja o volume do sólido obtido pela rotação em torno do eixo da região limitada por e . Encontre pelo método de fatiamento e cascas cilíndricas. Em ambos os casos, desenhe um diagrama para explicar seu método.
Passo 1
Pelo método de fatiamento temos os seguintes esboços:
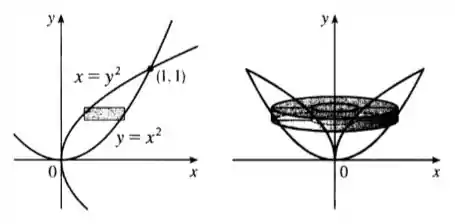
Aqui houve uma transformação na função elevando os dois lados ao quadrando, chegando na função .
Calculando o volume:
Passo 2
Calculando pelo método das cascas cilíndricas temos o desenho seguinte:
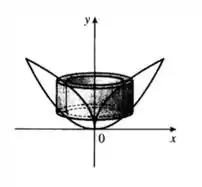
Calculando o volume:
Resposta
.
Exercícios de Livros Relacionados
Use camadas cilíndricas para encontrar o volume do sólido que é gerado quando a região envolvida por y = x 3 , y = 1 ,x = 0 gira em torno da reta y = 1 .
Nas partes ( a ) a ( c ) , encontre o volume do sólido cuja base é o interior do círculo x 2 + y 2 = 1 e cujas seções transversais tomadas perpendicularmente à base são a Semicírculos b Quadrados ( c
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d
Descreva o método do fatiamento para encontrar volumes e use-o para deduzir uma fórmula integral para obter volumes pelo método dos discos.
Enuncie uma fórmula integral para encontrar um volume pelo método das camadas cilíndricas e use somas de Riemann para derivar a fórmula dada.