Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 1.3 - Ex. 29
Siga os passos indicados aqui para deduzir a equação de movimento de um pêndulo, Eq. (12) no texto. Suponha que a barra do pêndulo é rígida e sem peso, que a massa é pontual e que não existe atrito ou resistência em nenhum ponto do sistema.
- Suponha que a massa está em uma posição deslocada arbitrária, indicada pelo ângulo . Desenhe um diagrama mostrando as forças que agem sobre a massa.
- Aplique a lei do movimento de Newton na direção tangencial ao arco circular sobre o qual a massa se move. Então, a força de tensão sobre a barra não aparece na equação. Note que é necessário encontrar a componente da força gravitacional na direção tangencial. Note também que a aceleração linear, em oposição à aceleração angular, é , em que é o comprimento da barra.
- Simplifique o resultado obtido no item (b) para obter a Eq. (12) do texto.
Passo 1
Para resolvermos esse problema vamos analisar as informações dadas no enunciado e tentar descrever uma equação que satisfaça todos os requisitos do problema. Depois vamos aplicar as condições de contorno de cada item para encontrar as informações pedidas. Vamos juntos para resolver!!
Passo 2
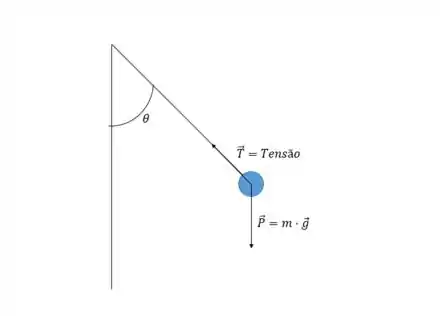
- Bom, vamos lá. Já que infelizmente o problema nos pede para aplicar a lei de Newton na tangencial, temos que será preciso aplicar uma mudança de variáveis. Agora nossas duas coordenadas serão . Temos que a lei de Newton nos diz que
- Se rearranjarmos os termos, dividirmos tudo pela massa e por , chegaremos que
Passo 3
Nessas novas coordenadas será algo parecido
Onde é a aceleração tangencial. Por sorte o próprio enunciado já nos diz qual é essa aceleração. Substituindo então ficamos com
Outra coisa importante que o enunciado nos diz é que a única forção que aparece na componente tangencial é a peso, então temos que
Se observarmos a projeção na componente tangencial, veremos que a componente da peso que será usada será a oposta ao ângulo, assim temos que:
Que é nossa equação
Passo 4
Resposta
(b)
(c)