Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 7.6 - Ex. 3
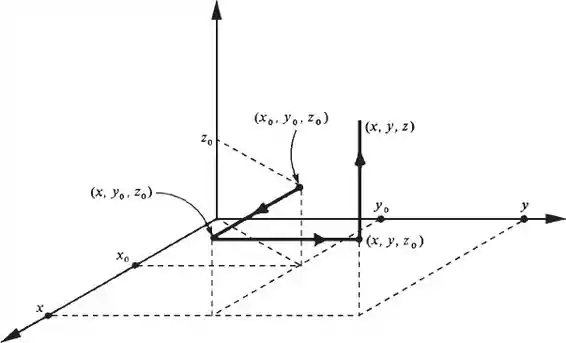
3) Suponha que o aberto Ω ⊂ ℝ2 tenha a seguinte propriedade: existe (x0,y0, z0) em Ω tal que, para todo (x, y, z) ∈ Ω, a poligonal de vértices (x0,y0, z0), (x, y0, z0), (x, y, z0) e (x, y, z) esteja contida em Ω
Seja de Casse no aberto e suponha que em . Seja
Prove que
Passo 1
Bem Para que F admita uma função potencial, tem que acontecer duas coisas. Nosso intervalo em R³ – – tem que ser simplesmente conexo e F ser independente de caminho, ou seja
Pelo que o enunciado nos diz, o espaço satisfaz as condições e Rot F =0. Então a principio sabemos que F admito uma função potencial. Vamos agora provar que essa função é
Passo 2
Vamos calcular
Sendo
Pelo enunciado sabemos que os termos que estamos integrando, por exemplo em
Esse x e y em não são variáveis, são números. Pode ate ficar confuso porque usaram a mesma letra, vamos trocar por para não confundir. De forma que vamos usar o Teorema fundamental do cálculo
Passo 3
Dessa forma temos que
E como
Podemos afirmar que
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)