55. Suponha que Prove que se e existem, então
Passo 1
Como o enunciado não nos traz muitas informações, devemos utilizar do conceito de derivada de função composta, função modular e uma relação fornecida já em exercícios anteriores que será fundamental para chegarmos na relação desejada.
Passo 2
A função modular nos permite estabelecer a seguinte relação
A partir dela podemos reescrever a função g(x) dada como
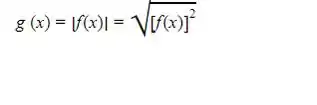
Passo 3
Derivando a função acima, observando que trata-se de uma função composta, temos
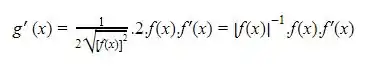
Passo 4
Aplicando o módulo em ambos os lados da equação
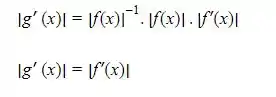
Resposta
Demonstração.