Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 48

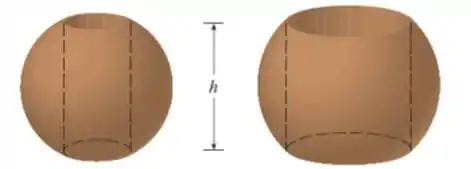
Suponha que você faça anéis para guardanapos perfurando buracos com diferentes diâmetros através de duas bolas de madeira (as quais têm diferentes diâmetros). Você descobre que ambos os anéis de guardanapo têm a mesma altura h , como mostrado na figura.

(a) Faça uma conjectura sobre qual anel tem mais madeira.

(b) Verifique sua conjectura. Use cascas cilíndricas para calcular o volume de uma anel de guardanapo criado pela perfuração de um buraco com raio r através do centro de uma esfera de raio R e expresse a resposta em termos de h .

Passo 1

Item a:

Quanto maior o Tamango da esfera, maior é o volume de madeira em cada anel.

Passo 2

Item b:

Se dividirmos o anel ao meio horizontalmente, pela simetria, temos a metade do volume de madeira do anel obtido pela rotação da parte superior da esfera de raio R dada pela curva f x = R 2 - x 2 limitada entre o raio r do buraco e o raio R de esfera.

Para calcularmos o volume do sólido de rotação em torno do eixo y da região sob a curva y = f ( x ) de a até b é

V = ∫ a b 2 π x f x d x ,     o n d e   0 ≤ a < b

Então, unido as duas metades do anel, temos que o volume é:

V = 2 ∫ r R 2 π x R 2 - x 2 d x

V = 4 π ∫ r R x R 2 - x 2 d x

Passo 3

Para ∫ x R 2 - x 2 d x , usamos u = R 2 - x 2 ⇒ d u = - 2 x   d x e obtemos:

∫ x R 2 - x 2 d x = ∫ - 1 2 u   d u = - 1 2 2 u 3 2 3 + C = u 3 2 3 + C = - R 2 - x 2 3 2 3 + C

Logo, o volume é dado por:

V = 4 π - R 2 - x 2 3 2 3 R r = 4 π 0 - - R 2 - r 2 3 2 3

V = 4 π R 2 - r 2 3 2 3

Pelo teorema de Pitágoras:

R 2 = r 2 + h 2 2

R 2 - r 2 = h 2 4

Então:

V = 4 π h 2 4 3 2 3

V = 4 π h 3 8 3 = π h 3 2 3

V = π h 3 6

Resposta

V = π h 3 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use as cascas cilíndricas para encontrar o volume do sólido. Uma esfera de raio r .
A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. y = - x 2 + 6 x - 8 ,y = 0 ; em torno do eixo x
A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. y = - x 2 + 6 x - 8 , y = 0 , e mt o r n od oe i x oy
A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = 1 - y 4 ,x = 0 ; em torno de x = 2
Use as cascas cilíndricas para encontrar o volume do sólido. O toro sólido do Exercício 63 da Seção 6.2.