Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.7 - Ex. 21
Teste a série quanto a convergência ou divergência.
21.
Passo 1
Oi, galera! Tudo show?
A questão pede pra gente analisar a série e classificar como convergente ou divergente.
Olha direitinho. Percebeu o ? Logo, a gente pode trabalhar com o Teste da Série Alternada!
Pra série alternada ser convergente, ela precisa obedecer a dois critérios:
Mas quem é nosso ?
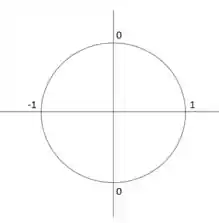
Reelembra que temos uma série alternada com valores entre e , já que no círculo trigonométrico só teremos valores para nesses pontos:
Passo 2
Temos que:
Então vamos aplicar o passo :
Se você substituir , vai ter os seguintes resultados:
E essa condição não se faz verdadeira. Vamos analisar a próxima:
Passo 3
Pela segunda condição:
Substituindo, como tende a zero, portanto:
Como o resultado deu , então pela segunda condição estamos diante, finalmente, de uma série divergente!