Trace a curva com equações paramétricas x = s e nt , y = s e n2 t , z = s e n3 t . Encontre o comprimento total desta curva com precisão de quatro casas decimais.

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.3 - Ex. 10

Trace a curva com equações paramétricas , , . Encontre o comprimento total desta curva com precisão de quatro casas decimais.

Passo 1

Chamando a curva de temos:

A curva pode ser traçada com o auxílio de um software, conforme vista abaixo:

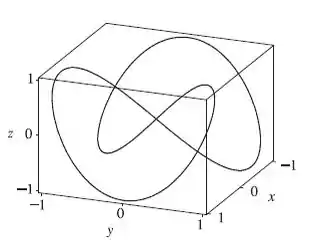
O comprimento de arco é dado pela fórmula geral:

Então deveremos derivar a equação de e deveremos também descobrir o intervalo de integração da nossa integral. A figura que foi traçada nos ajudará a encontrar o intervalo de integração, mas note que a nossa curva é periódica, até pelas funções periódicas que compõem sua equação paramétrica. Então descobrindo o período da nossa função, conseguiremos encontrar o intervalo de integração.

Passo 2

Observamos, pelo traçado da curva e por suas componentes, que se trata de uma função vetorial periódica. Analisando o período de cada uma de suas funções componentes, percebe-se que o maior deles é o da função , sendo igual à . Por isso, concluímos que a curva completa é dada para o intervalo do parâmetro igual à .

O comprimento de arco é dado pela fórmula geral:

Para a função tratada nesse exercício temos

Passo 3

Para calcular o comprimento precisaremos da derivada da curva. Assim, temos:

Obtida , podemos calcular seu módulo:

Passo 4

Obtido o módulo da derivada, substituímos o valor na fórmula do comprimento de arco:

Utilizando uma calculadora avançada ou um software é possível obter a aproximação da integral acima. Obtemos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Trace a curva com equações paramétricas x = 1 + cos ⁡ 16 t cos ⁡ t,y = 1 + cos ⁡ 16 ts e nt,z = 1 + cos ⁡ 16 t Explique a aparência da curva, mostrando que ela está em um cone.

Utilize um computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva. r t = t ,e t , cos ⁡ t

Mostre que a curva com equações paramétricas x = t 2,y = 1 - 3 t,z = 1 + t 3 passa pelos pontos 1 ,4 ,0 e 9 ,- 8 ,28 , mas não passa pelo ponto 4 ,7 ,- 6 .

Tente esboçar à mão a curva obtida pela intersecção do cilindro circular x 2 + y 2 = 4 com o cilindro parabólico z = x 2 . Determine então as equações paramétricas dessa curva e utilize um computador

Trace a curva com equações paramétricas x = 1 - 0,25 cos 2 ⁡ 10 t cos ⁡ t,y = 1 - 0,25 cos 2 ⁡ 10 t s e nt,z = 0,5 cos ⁡ 10 t Explique a aparência da curva, mostrando que ela está em uma esfera.