Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.Revisão - Ex. 51
Se A unidades quadradas for a área de um triângulo retângulo isósceles cujos catetos têm x unidades de comprimento, ache (a) a taxa média de variação de A em relação a x quando x varia de 8,00 para 8,01; (b) a taxa de variação instantânea de A em relação a x, quando x é 8,00
Passo 1
Bom, para encontrarmos as duas taxas pedidas, vamos precisar encontrar primeiro a equação que descreve a área do nosso triângulo. Como sabemos q ele é retângulo, com os dois catetos com comprimento x, sabemos que a base do triângulo é a hipotenusa. Pelo Teorema de Pitágoras:
Onde b é a base.
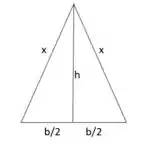
Para acharmos a altura, imagine o triângulo cortado no meio, e a metade da base e a altura passarão a ser os catetos do novo triângulo retângulo. Pelo Teorema de Pitágoras:
Sendo h a altura. Substituindo b:
A altura será:
Agora pela área do triângulo:
Substituindo b e h:
Passo 2
Agora que temos a equação A, precisamos apenas calcular a razão entre a variação de A e a variação de x para obtermos a taxa média de A pedida na letra (a):
Passo 3
Para a letra (b) precisamos calcular a derivada da função A, pois a questão pede a taxa instantânea em relação a x:
Substituindo o valor dado de x: