Exercícios de Otimização – Modelagem - Lista de Exercícios Resolvida
Questão 1
Se um objeto dista unidades de um foco de intensidade luminosa constante , a luminosidade do objeto é igual a . Dois focos, e com intensidades e , respectivamente, encontram-se separados por unidades. Em que ponto do segmento de reta liga a , a luminosidade é mínima? Qual deve ser a razão entre e para que o ponto de luminosidade mínima entre os dois focos esteja a uma distância de unidades da fonte de luminosidade ?
Ver solução completaQuestão 2
Um quadro de altura está pendurado em uma parede vertical de modo que sua borda inferior está a uma altura do raio de visão horizontal de um observador. A que distância da parede deve colocar-se o observador para que a sua posição seja a mais vantajosa para contemplar o quadro, isto é, para que o ângulo de visão seja máximo?
Ver solução completaQuestão 3
Um triângulo retângulo, localizado no primeiro quadrante, tem um vértice na origem e seus outros dois vértices determinados pela interseção da reta tangente ao gráfico da função com os eixos coordenados (ver figura).
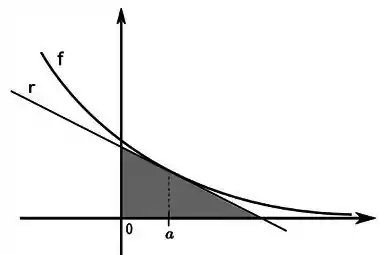
Determine a equação da reta tangente ao gráfico da em .
Determine as interseções da reta com o eixo e com o eixo .
Determine o valor de de forma que a área do triângulo seja máxima, considerando somente os triângulos formados no quadrante.
Ver solução completaQuestão 4
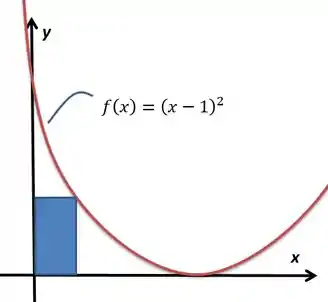
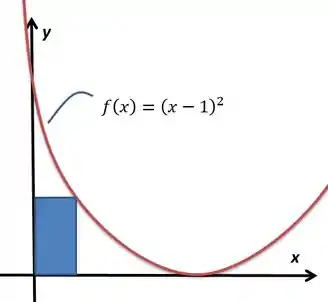
Dentre os retângulos limitados pelo eixo , pelo eixo e pelo gráfico de definida por (conforme a figura), determine as dimensões do retângulo de área máxima.
Questão 5
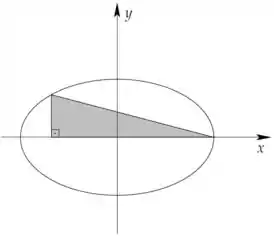
Considere a elipse de equação e todos os triângulos retângulos construídos com um dos vértices em , um sobre a elipse e o terceiro sobre o eixo , como na figura abaixo. Justifique a existência, dentre esses triângulos, de um com área máxima e determine as medidas de sua base e sua altura.
Questão 6
Dentre os retângulos limitados pelo eixo , pelo eixo e pelo gráfico de definida por (conforme a figura), determine as dimensões do retângulo de área máxima.
Questão 7
Forma-se um triângulo retângulo no primeiro quadrante com vértice na origem e no qual a hipotenusa é um segmento de reta tangente ao gráfico de , cujas extremidades estão sobre os eixos coordenados.
Existe uma área máxima para tal triângulo? Existe uma área mínima? Justifique.
Qual o comprimento da menor hipotenusa desta família de triângulos? Certifique-se de que sua resposta dê o mínimo global.
Ver solução completaQuestão 8
Um oleoduto tem a forma de curva com , e medidos em quilômetros. Será construída uma cerva tangente à curva no ponto . Determine as coordenadas do ponto de modo que a área da região triangular formada pela cerva e pelos eixos seja mínima.
Ver solução completaQuestão 9
Encontre o menor segmento de reta contido no primeiro quadrante ligando o eixo ao eixo e passando pelo ponto .
Ver solução completaQuestão 10
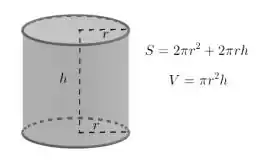
Um cilindro circular reto fechado de altura e raio das bases tem área total igual a e volume . DENTRE TODOS OS CILINDROS DE VOLUME , obtenha as dimensões daquele que tem a menor área total possível.
Questão 11
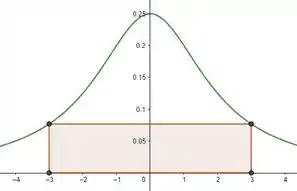
Encontre a maior área de um retângulo que podemos inscrever entre o gráfico da função e o eixo das abscissas . Justifique por que o retângulo que você encontrou será o de maior área.
Questão 12
Sejam . Determine, caso exista, o perímetro mínimo dos triângulos de base e altura (relativa à base dada) .
Ver solução completaQuestão 13
Encontre a área do maior retângulo que pode ser inscrito dentro da região delimitada pela parábola e pelo eixo , fronteira incluída.
Ver solução completaQuestão 14
Uma página deve conter de área impressa. As margens superior e inferior devem ter , enquanto as laterais têm cada. Encontre as dimensões da página que consomem a menor quantidade de papel.
Ver solução completaQuestão 15
Determine o retângulo de área máxima e lados paralelos aos eixos coordenados, inscrito na elipse
Ver solução completaQuestão 16
Considere os cones circulares retos inscritos numa esfera de raio cujas alturas variam no intervalo . Entre esses cones, sejam o de menor volume e o de maior volume. Então a razão entre o volume de e o volume de é
Questão 17
Um quadro de altura está pendurado em uma parede vertical de modo que sua borda inferior está a uma altura do raio de visão horizontal de um observador. A que distância da parede deve colocar-se o observador para que a sua posição seja a mais vantajosa para contemplar o quadro, isto é, para que o ângulo de visão seja máximo?
Ver solução completaQuestão 18
Um contêiner retangular sem tampa para estocagem deve ter volume de O comprimento de sua base é o dobro de sua largura. O material para a base custa e o material para as laterais custa . Encontre o custo dos materiais para o barato desses contêiners. Não esqueça de verificar que de fato esse é o mais barato dos contêiners!
Ver solução completaQuestão 19
3) Na figura, as semirretas e são paralelas e o segmento é perpendicular a essas semirretas. O ponto , situado no segmento , é tal que: e . Considere a coleção de todos os triângulos retângulos , com ângulo reto em , tais que está sobre a semirreta e está sobre a semirreta .
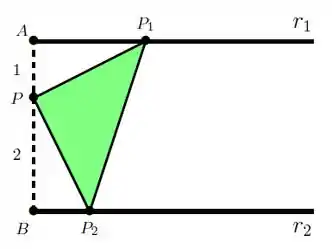
Determine a menor área possível para um triângulo dessa coleção:
Ver solução completaQuestão 20
3) Um retângulo tem os dos vértices inferiores sobre o eixo e os dois vértices superiores pertencentes à curva . Dentre todos os retângulos nestas condições, quais as dimensões daquele que tem a maior área? Justifique sua resposta!
Ver solução completaQuestão 21
Uma caixa sem tampa deve ser construída a partir de um quadrado de de largura, cortando fora um quadrado de cada um dos quatro cantos e dobrando para cima os lados. Encontre o maior volume que essa caixa pode ter. Justifique detalhadamente porque o máximo existe.
Ver solução completaQuestão 22
Seja um ponto da parábola , com .
- Escreva uma função que represente a área do triângulo determinado pelos pontos , e .
- Encontre o valor de tal que a área do triangulo do item anterior seja máxima. Justifique sua resposta!
Questão 23
1) Seja a região limitada do plano, compreendida entre a parábola e o eixo . Considere um trapézio isóscele contido em com as seguintes propriedades:
- A base maior é o segmento do eixo ;
- Os vértices da base menor também estão situados no gráfico da parábola (ver figura abaixo)
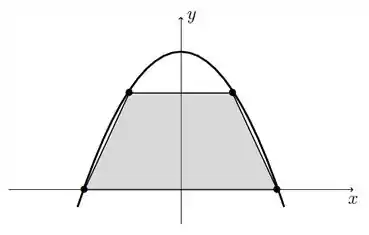
Qual a maior área possível que este trapézio pode ter?
Ver solução completaQuestão 24
Um trapézio é inscrito num circulo de raio , de modo que a base do trapézio é o diâmetro do círculo. Sabendo que o trapézio de área máxima tem área , podemos concluir que a área do disco de raio é
.
.
.
.
.
Ver solução completaQuestão 25
O volume máximo do cilindro circular reto que pode ser inscrito numa esfera de raio é igual a
Ver solução completaQuestão 26
Encontre dois números positivos cujo produto seja 100 e cuja soma seja mínima.
Ver solução completaQuestão 27
Uma lata cilíndrica é feita para receber um litro de óleo. Encontre as dimensões que minimizarão o custo do metal para produzir a lata.
Ver solução completaQuestão 28
Uma janela normanda tem o formato de justaposição de um semicírculo sobre um retângulo. Suponha que o perímetro da janela normanda é de .
a) Determine a área da janela como função da altura do retângulo correspondente.
b) Ache as dimensões da janela com maior área possível, assim como a área desta janela (aplique os conceitos do cálculo diferencial).
Ver solução completaQuestão 29
Considere os cones circulares retos inscritos numa esfera de raio cujas alturas variam no intervalo . Entre esses cones, sejam o de maior volume e o de menor volume. Então a razão entre o volume de e o volume de é
Questão 30
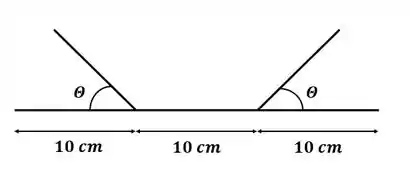
Uma calha deve ser construída com uma folha de metal de largura , dobrando-se para cima da folha de cada lado, fazendo-se um ângulo com a horizontal. Como deve ser escolhido de forma que a capacidade de carregar a água na calha seja máxima?
Questão 31
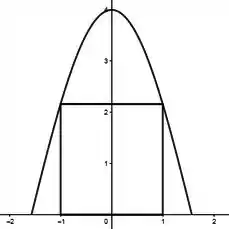
Considere a região . Determine as dimensões do retângulo de maior perímetro possível que pode ser inscrito em .
Questão 32
Determine as dimensões do retângulo com lados paralelos aos eixos coordenados que tenha área máxima, sabendo que o retângulo está inscrito na região limitada pelas parábolas e
Ver solução completaQuestão 33
Se um objeto dista unidades de um foco de intensidade luminosa constante , a luminosidade do objeto é igual a . Dois focos, e com intensidades e , respectivamente, encontram-se separados por unidades. Em que ponto do segmento de reta liga a , a luminosidade é mínima? Qual deve ser a razão entre e para que o ponto de luminosidade mínima entre os dois focos esteja a uma distância de unidades da fonte de luminosidade ?
Ver solução completaQuestão 34
Um triângulo retângulo, localizado no primeiro quadrante, tem um vértice na origem e seus outros dois vértices determinados pela interseção da reta tangente ao gráfico da função com os eixos coordenados (ver figura).
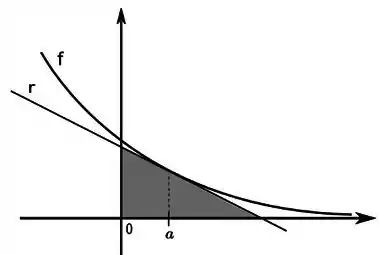
Determine a equação da reta tangente ao gráfico da em .
Determine as interseções da reta com o eixo e com o eixo .
Determine o valor de de forma que a área do triângulo seja máxima, considerando somente os triângulos formados no quadrante.
Ver solução completaQuestão 35
Q02) Um comerciante deseja produzir uma ampulheta para venda em sua loja. A ampulheta será composta de dois cones idênticos, unidos pelo vértice. O comerciante planeja construir a ampulheta de vidro e em seguida fechar as bases com uma tampa de metal. Ele também planeja que a área superficial da ampulheta, excetuando-se as tampas de metal,seja de . Qual deve ser o raio da tampa para que a ampulheta possa marcar o maior intervalo de tempo possível?
Dica: A área lateral de um cone de raio e altura é dada por .
Ver solução completaQuestão 36
Considere os cones circulares retos inscritos numa esfera de raio cujas alturas variam no intervalo . Entre esses cones, sejam o de menor volume e o de maior volume. Então a razão entre o volume de e o volume de é
Questão 37
Determine as dimensões do retângulo inscrito no semicírculo de raio e que tem o maior perímetro. Justifique sua resposta.
Ver solução completaQuestão 38
Considere os cones circulares retos inscritos numa esfera de raio cujas alturas variam no intervalo . Entre esses cones, sejam o de maior volume e o de menor volume. Então a razão entre o volume de e o volume de é
Questão 40
Seja . Considere o triangulo com vértices em , e . Ache o valor de que maximize o ângulo entre e .
Ver solução completaQuestão 41
Um fabricante produz por semana toneladas de um certo produto. O preço de venda é de unidades monetárias por tonelada do produto e está relacionado com por , . O custo de produção é de unidades monetárias. Determine para que o lucro seja máximo. Determine, também, o lucro máximo.
Ver solução completaQuestão 42
Determine o retângulo de área máxima, e lados paralelos aos eixos coordenados inscritos na elipse de equação
Ver solução completaQuestão 43
Q03) Deseja-se construir um reator nuclear em uma usina elétrica. O reator tem formato cilíndrico e será instalado dentro de uma cúpula semi-esférica de raio igual a , conforme ilustra a figura abaixo. Determine o raio da base do cilindro de maior volume que pode ser instalado dentro da cúpula.
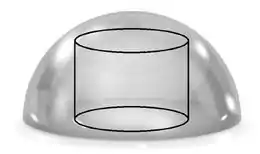
Questão 44
Se um objeto de massa m é solto a partir do repouso, um modelo para sua velocidade v após t
segundos, levando-se em conta a resistência do ar, é
onde g é a aceleração da gravidade e c é uma constante positiva. (a) Calcule
Qual o significado desse limite?
Ver solução completaQuestão 45
Se um retângulo tiver sua base em um eixo e dois vértices sobre a curva . Mostre que o retângulo tem maior área possível quando os vértices estão nos pontos de inflexão da curva.
Ver solução completa