Use cortes para esboçar e identificar as superfícies.
Passo 1
Beleza, galera? Primeiro, vamos fazer os cortes, igualando cada variável a uma constante arbitrária . Vamos começar com :
- :
- :
- :
Então esse corte é uma hipérbole, pra .
Passo 2
Continuando:
Aqui temos uma parábola, com concavidade voltada para o sentido negativo do eixo .
Novamente temos uma parábola, mas agora com concavidade voltada para o sentido positivo do eixo .
Passo 2
Show! Juntando todas essas informações, podemos esboçar a superfície:
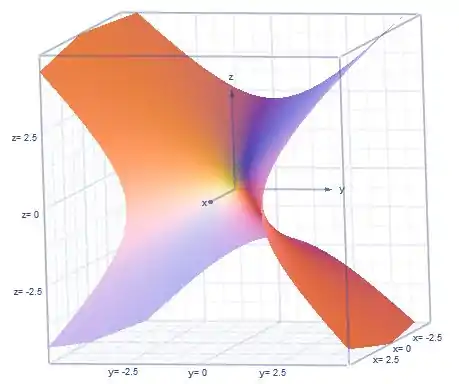
Veja que isso é um paraboloide hiperbólico, ok?
Resposta
Paraboloide hiperbólico