Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Equação Do Plano

Ver Todos os Exercícios

Teoria

Um plano é um objeto geométrico de duas dimensões. Mas.. você sabe como achar a equação de um plano?

Como Calcular a Equação de um Plano

Um plano é tipo uma folha de papel infinita suspensa no espaço, ele tem essa carinha aqui:

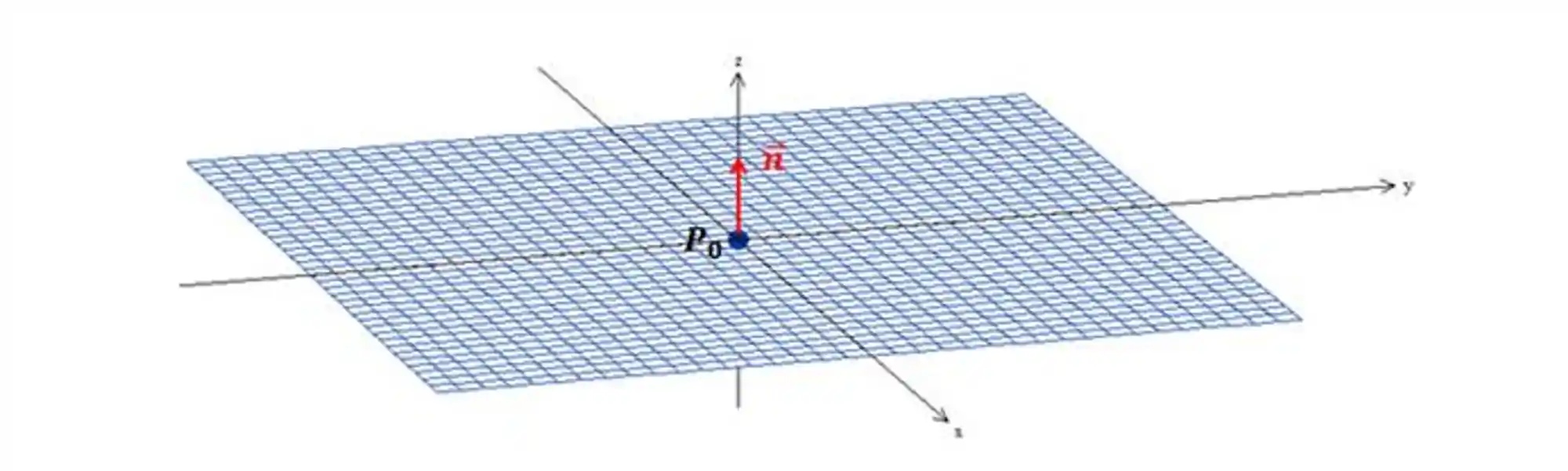
Plano
Plano

Para um plano ser definido no espaço, precisamos apenas de duas informações, que são super importantes: um ponto que pertença ao plano e um vetor normal ao plano, que serve para a gente definir a sua direção.

📢 Clique para saber mais:

Equação do Plano

Mas agora vamos ao que interessa! A equação de um plano com um vetor normal , um ponto é dada por:

Vamos ver um exemplo! Imagine um vetor normal ao plano , um ponto , e um ponto qualquer no plano . Assim:

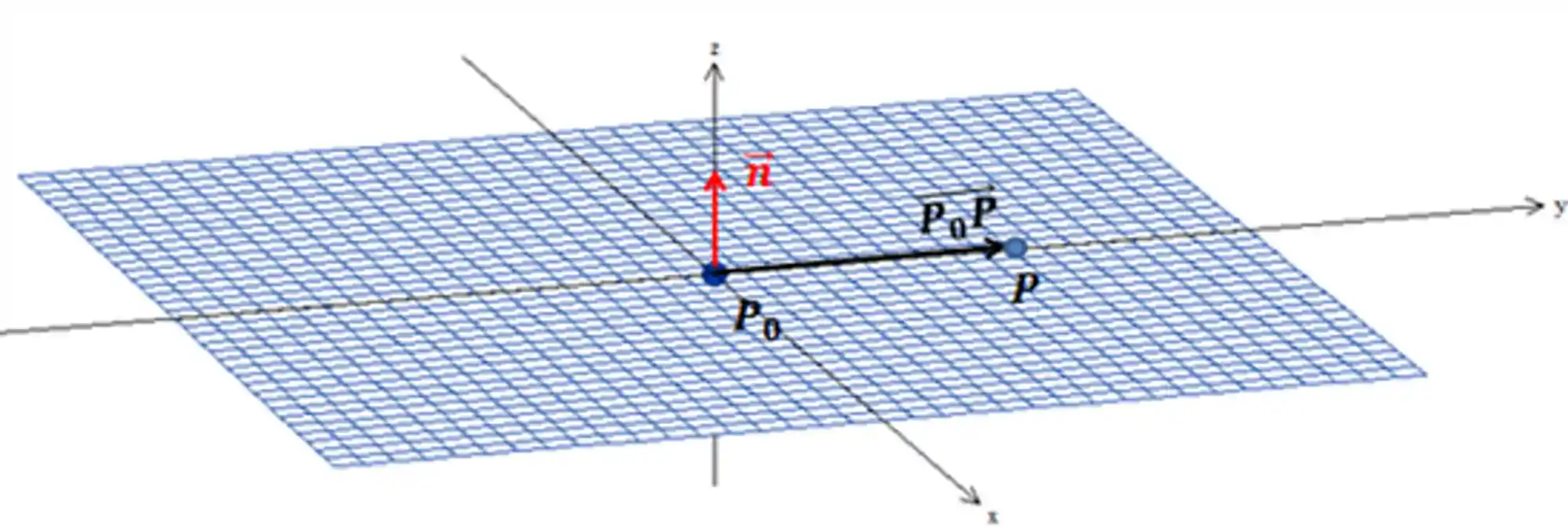
Exemplo: Como achar a equação de um plano
Exemplo: Como achar a equação de um plano

O vetor está contido no plano e tem componentes . O vetor é normal ao plano e, portanto, ortogonal a qualquer vetor contido no plano. Logo o vetor é ortogonal ao vetor .


O produto escalar entre dois vetores ortogonais é zero. Então o produto escalar entre o vetor e o vetor é zero!!! Logo o produto escalar fica assim:

Confira esse conteúdo em vídeo:

Equações Paramétricas do Plano

A equação paramétrica de um plano pode ser calculada a partir das seguintes equações:

Equações Paramétricas do Plano
Equações Paramétricas do Plano

Onde e são os parâmetros da equação.

Gráfico do Plano

Já sabemos encontrar a equação do plano. Show! Mas e se pedirem o gráfico do plano?! Vamos ver agora um passo a passo de como fazer isso.

Para isso vamos considerar o plano

Passo 1: Traços

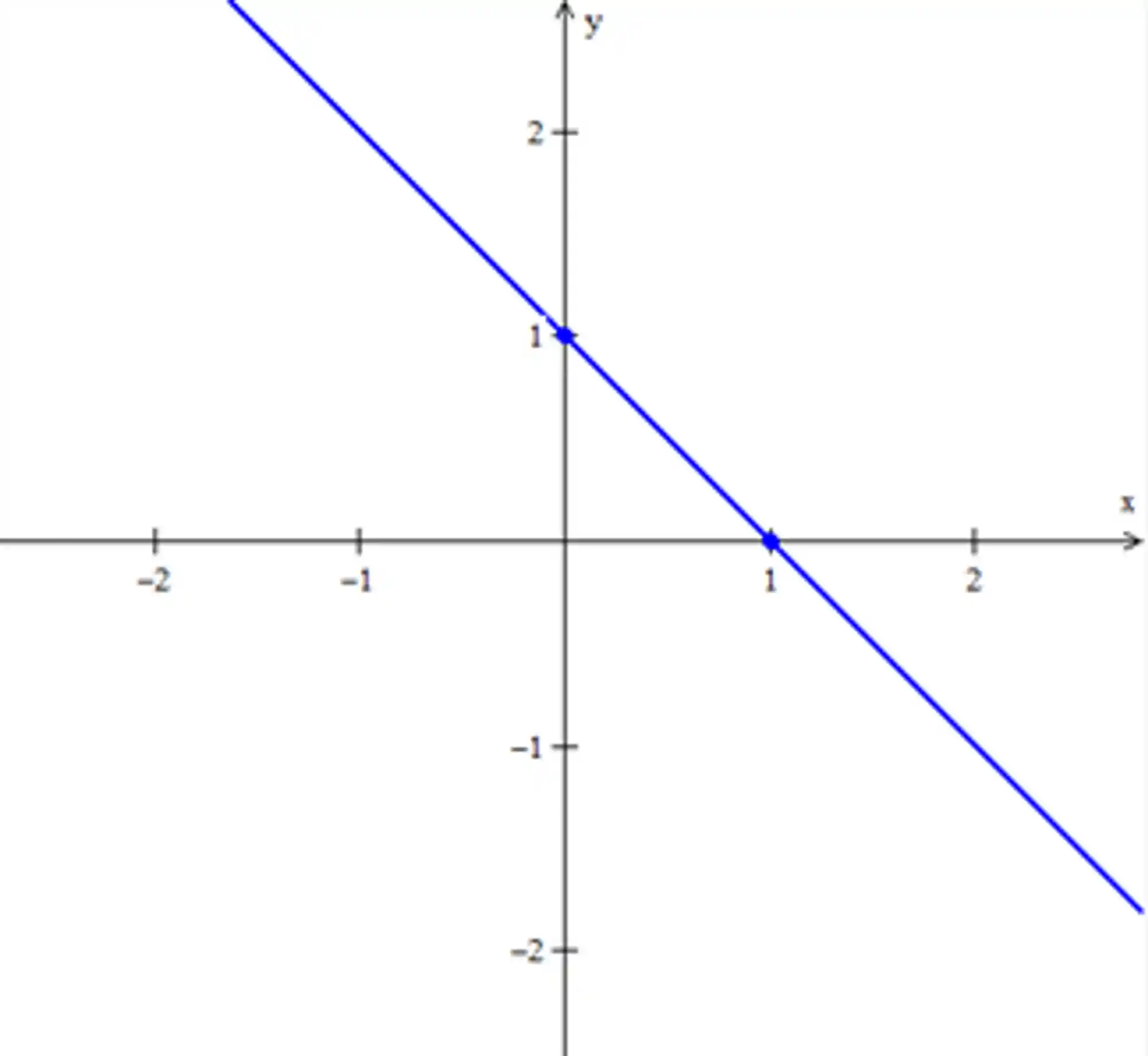
A primeira coisas que vamos fazer é os traços do plano dado. O traço de um plano, ou qualquer outra superfície, são as curvas de interseção entre o plano e os planos coordenados , e . Vamos começar achando o traço para o plano , para isso fazemos:

Essa reta intercepta o eixo no ponto e intercepta o eixo no ponto .Portanto, o traço no plano fica:

Traço no plano xy.
Traço no plano xy.

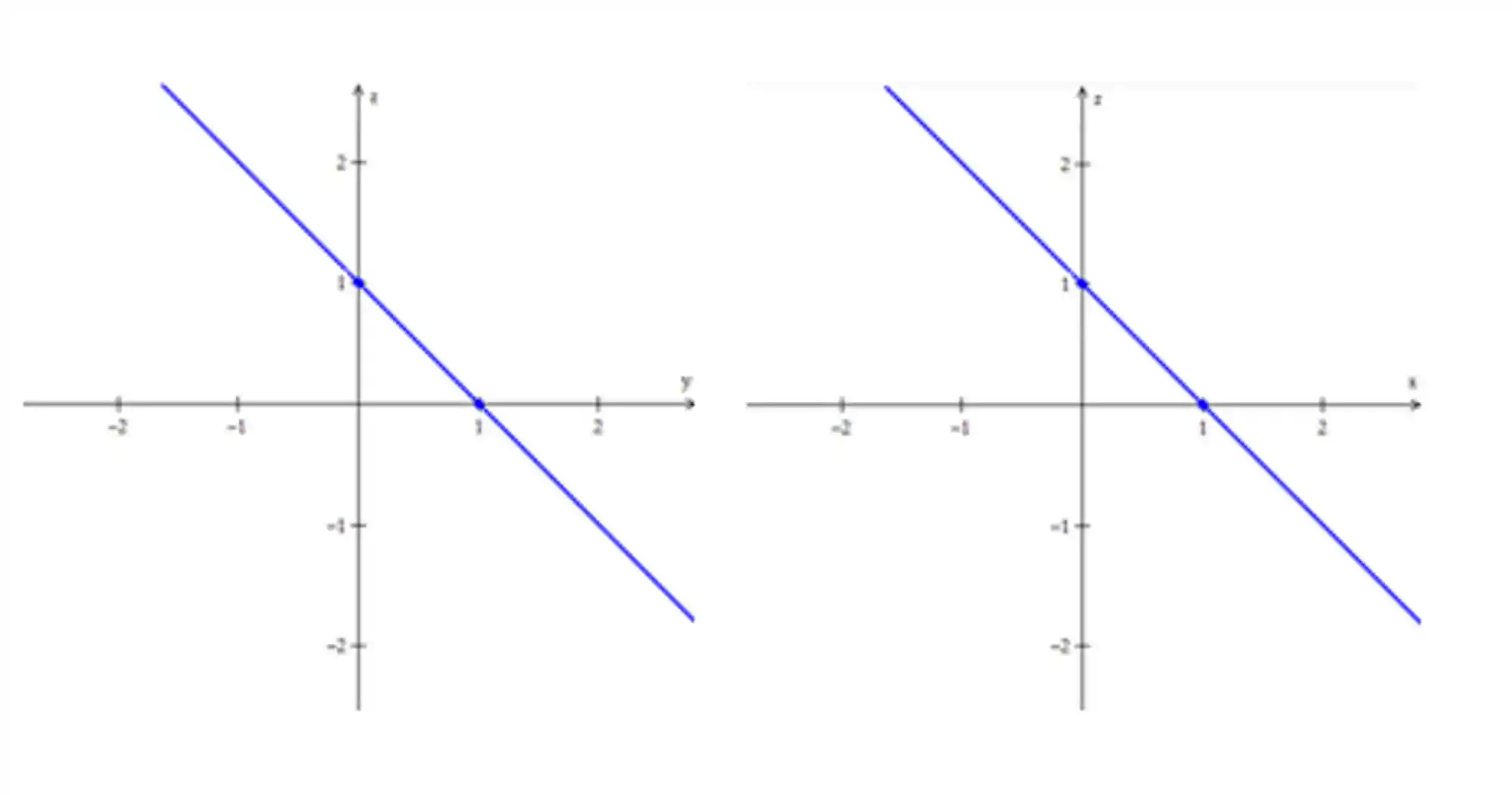
Agora fazemos o mesmo para os planos e , chegamos em:

Traços no plano yz e xz.
Traços no plano yz e xz.

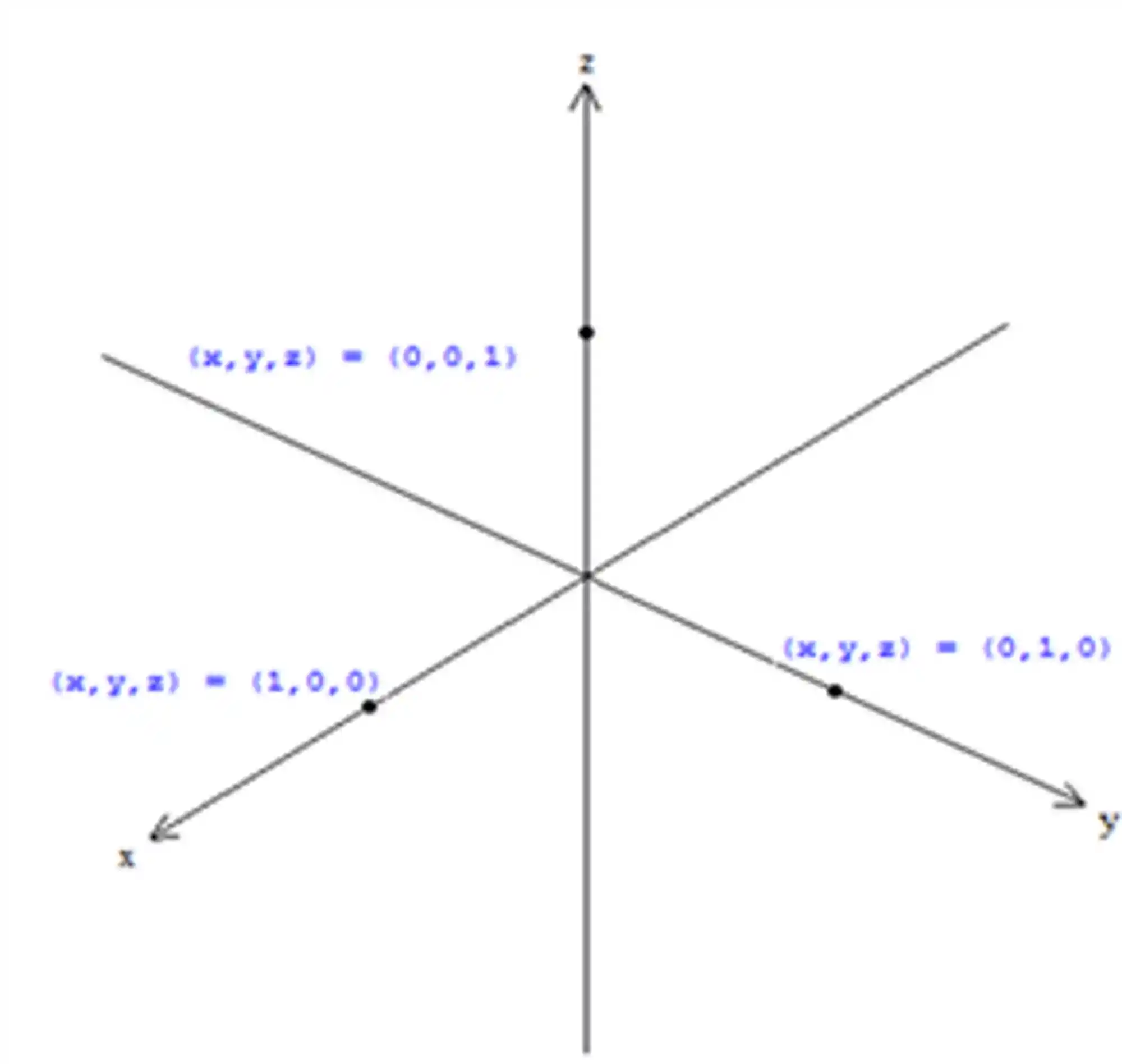
Passo 2: Marcar os pontos de interseção do plano com os eixos coordenados.

O próximo passo é marcar nos 3 eixos coordenados os pontos que achamos nos traços acima. Os pontos são: (1,0,0), (0,1,0) e (0,0,1). Fica:

interseção do plano com os eixos coordenados
interseção do plano com os eixos coordenados

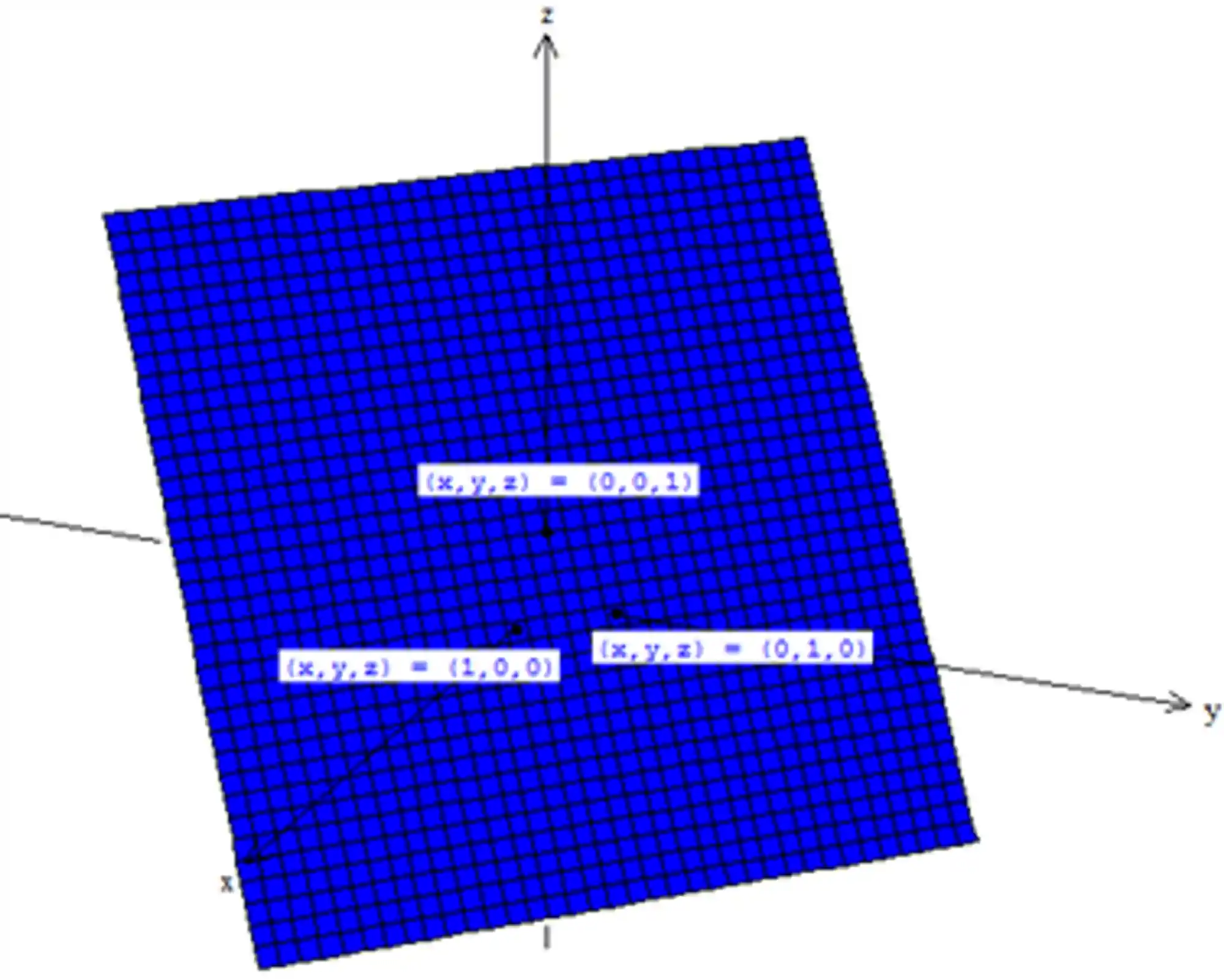
Passo 3: Traçar um paralelograma e hachura-lo

Agora traçamos um paralelogramo passando sobre os pontos e hachura esse paralelogramo. Repare que ele é inclinado para a esquerda, devido ao traço no plano ser uma reta também inclinada para a esquerda. Então o esboço do plano fica assim:

Esboço do plano
Esboço do plano

Agora vamos praticar com exercícios?

Gráfico do Plano

Exercícios Resolvidos

Exercício Resolvido #1

Georg B. Thomas, Cálculo Volume 2, 11ª ed. São Paulo: PEARSON education do Brasil, 2009, pp. 207 - 26

Encontre a equação do plano que passa por A = ( 1 , - 2,1 ) e é perpendicular ao vetor da origem até A , e esboce seu gráfico.

Passo 1

Para encontrar a equação do plano, precisamos de dois elementos:

  • Um ponto P 0 pertencente ao plano.
  • E um vetor normal ao plano n →

O problema já fornece diretamente um ponto pertencente ao plano P 0 = A = ( 1 , - 2,1 ) .

Passo 2

Agora, temos de encontrar o vetor normal ao plano. Porém, podemos achá-lo calculando o vetor O A → , que é o vetor que vai da origem até A .

Calculando O A → :

n → = O A → = 1 , - 2,1 - 0,0 , 0 = 1 , - 2,1

Passo 3

Agora basta encontrar a equação do plano:

n → = a , b , c = 1 , - 2,1

P 0 = x 0 , y 0 , z 0 = ( 1 , - 2,1 )

a x - x 0 + b y - y 0 + c z - z 0 = 0

1 x - 1 - 2 y - - 2 + 1 z - 1 = 0

x - 1 - 2 y - 4 + z - 1 = 0

x - 2 y + z = 6

Passo 4

Vamos fazer os traços do plano.

  • Traço no plano x y ( z = 0 ) :

    • y = x - 6 2

    O eixo x   é interceptado no ponto ( 6,0 , 0 ) e o eixo y também tem um ponto de

    interseção em ( 0 , - 3,0 )

  • Traço no plano y z ( x = 0 ) :

    • z = 6 + 2 y

    O eixo z   é interceptado no ponto ( 0 , 0,6 ) e o eixo y também tem um ponto de interseção em ( 0 , - 3,0 )

  • Traço no plano z x ( y = 0 ) :

z = 6 - x

O eixo x   é interceptado no ponto ( 6 , 0,0 ) e o eixo z também tem um ponto de interseção em ( 0,0 , 6 )

Passo 5

Marcando os pontos , fazendo o paralelogramo, hachurando sua área, o gráfico fica:

Resposta

A equação do plano é:

x - 2 y + z = 6

E o seu esboço:

Exercício Resolvido #2

Georg B. Thomas, Cálculo Volume 2, 11ª ed. São Paulo: PEARSON education do Brasil Ltda, 2009, pp. 207 - 24

Encontre a equação do plano que passa por A = 2,4 , 5 , B = 1,5 , 7 e C = - 1,6 , 8 e esboce seu gráfico.

Passo 1

Para encontrar a equação do plano precisamos do vetor normal n → e de um ponto pertencente ao plano. Beleza?

O problema nos fornece 3 pontos pertencentes ao plano. Ou seja, só nos falta encontrar o vetor normal n →

Vamos começar encontrando vetores pertencentes ao plano.

A B → = 1,5 , 7 - 2,4 , 5 = - 1,1 , 2

A C → = - 1,6 , 8 - 2,4 , 5 = ( - 3,2 , 3 )

Passo 2

Temos dois vetores pertencentes ao plano: A B → e A C →

Se fizermos o produto vetorial entre eles, teremos um vetor que é simultaneamente ortogonal a : A B → e A C → , e consequentemente normal ao plano. Então temos:

n → = A B → ×   A C → = i ^ j ^ k ^ - 1 1 2 - 3 2 3 = 3 - 4 i ^ - - 3 - - 6 j ^ + - 2 - - 3 k ^ = - i ^ - 3 j ^ + k ^

Passo 3

Pronto!!! Temos um vetor normal ao plano. Agora é só montar a equação do plano. Mas qual ponto eu escolho para utilizar como ponto pertencente ao plano na equação??? Qualquer um. Tanto faz. Vou escolher o ponto A . Temos:

n → = a , b , c = - 1 , - 3,1

P 0 = A = x 0 , y 0 , z 0 = ( 2,4 , 5 )

a x - x 0 + b y - y 0 + c z - z 0 = 0

- 1 x - 2 - 3 y - 4 + 1 z - 5 = 0

- x - 3 y + z = - 9

Passo 4

Vamos fazer os traços do plano.

  • Traço no plano x y ( z = 0 ) :

    • y = 9 - x 3

    O eixo x   é interceptado no ponto ( 9,0 , 0 ) e o eixo y também tem um ponto de

    interseção em ( 0,3 , 0 )

  • Traço no plano y z ( x = 0 ) :

    • z = 3 y - 9

    O eixo z   é interceptado no ponto ( 0,0 , - 9 ) e o eixo y também tem um ponto de interseção em ( 0,3 , 0 )

  • Traço no plano z x ( y = 0 ) :

z = x - 9

O eixo x   é interceptado no ponto ( 9,0 , 0 ) e o eixo z também tem um ponto de interseção em ( 0,0 , - 9 )

Passo 5

Marcando os pontos , fazendo o paralelogramo, hachurando sua área, o gráfico fica:

Resposta

A equação do plano é:

x + 3 y - z = 9

E o seu esboço:

Exercício Resolvido #3

UFRJ - Cálculo 2 - PF 2013.2 - ME1

A equação do plano que contém as 2 retas parametrizadas por

r 1 t = 1 + t ,   t ,   - 1 + t ,         r 2 t = 1 - t ,   2 t ,   - 1 + t ,

com t ∈ R , é:

(a) x + y + z = 0

(b) - x - 2 y + 3 z = - 4

(c) - x + 2 y + z = 0

(d) - x - 2 y + 3 z = 0

(e) Nenhuma das demais alternativas.

Passo 1

A equação de um plano que passa pelo ponto P 0 e tem vetor normal n → é dada por: n → = a , b , c

P 0 = x 0 , y 0 , z 0

a x - x 0 + b y - y 0 + c z - z 0 = 0

Então precisamos de um ponto onde o plano passa e de um vetor normal do plano!

Passo 2

Eles nos deu parametrizações de duas retas.

A parametrização de uma reta é da forma

r t = P 1 + v → t

onde P 1 é um ponto da reta e v → um vetor na direção da reta.

Repare que

r 1 t = 1,0 , - 1 + 1,1 , 1 t     e     r 2 t = 1,0 , - 1 + - 1,2 , 1 t

Ou seja, as 2 retas se cruzam no ponto ( 1,0 , - 1 ) e depois uma parte na direção do vetor v 1 → = ( 1,1 , 1 ) e a outra na direção do vetor v 2 → = ( - 1,2 , 1 ) .

Então já achamos um ponto do plano: o ponto P 0 = ( 1,0 , - 1 )

Na real, elas serem concorrentes foi uma grande coincidência! Caso elas não tivessem um ponto em comum, bastaria pegar qualquer ponto de uma das retas para ser o nosso P 0 . Afinal elas estão contidas no plano, ou seja, todos os pontos da reta, são pontos do plano!

Passo 3

Além do mais, isso que descobrimos é ótimo pra achar o vetor normal do plano!

Esse vetor n → é normal ao plano, então ele é normal às duas retas. Ou seja, ele é ortogonal aos vetores diretores dessas retas v 1 → = ( 1,1 , 1 ) e v 2 → = ( - 1,2 , 1 ) .

Fazendo o produto vetorial entre esses dois vetores, vamos encontrar n → , o vetor normal a esses dois vetores e consequentemente normal ao plano. Então temos:

n → = v 1 → x v 2 → = i ^ j ^ k ^ 1 1 1 - 1 2 1 = 1 x 1 - 2 x 1 i ^ - 1 x 1 - - 1 x 1 j ^ + 1 x 2 - - 1 x 1 k ^ = - i ^ - 2 j ^ + 3 k ^

n → = - 1 , - 2,3

Passo 4

Show! Vamos aplicar a equação do plano:

n → = a , b , c = - 1 , - 2,3

P 0 = x 0 , y 0 , z 0 = ( 1,0 , - 1 )

a x - x 0 + b y - y 0 + c z - z 0 = 0

- 1 x - 1 - 2 y - 0 + 3 z - - 1 = 0

- x - 2 y + 3 z = - 4

Resposta

Alternativa (b)

Exercício Resolvido #4

Georg B. Thomas, Cálculo Volume 2, 11ª ed. São Paulo: PEARSON education do Brasil Ltda, 2009, pp. 208 - 70

Encontre a equação de um plano N que passa pela origem e encontra o plano M : 2 x + 3 y + z = 12 em um ângulo reto.

Passo 1

O problema de cara já fornece um ponto pertencente ao plano N cuja equação queremos encontrar: P 0 = ( 0,0 , 0 )

Falta encontra o vetor normal ao plano N

Passo 2

Vamos achar esse vetor normal à N : n → = ( a , b , c )

O problema afirma que o plano N é ortogonal ao plano M , isso faz com que o vetor normal n → também seja ortogonal a m → (vetor normal ao plano M ).

Agora como achar m → ? Po, a equação do plano não é:

a x - x 0 + b y - y 0 + c z - z 0 = 0

Então concorda comigo que os coeficientes que multiplicam x , y , z são as componentes do vetor normal? Portanto, olhando a equação do plano M a gente conclui que o vetor normal m → é:

m → = ( 2,3 , 1 )

Passo 3

Como n → e m → são ortogonais, então:

n → ⋅ m → = 0

a , b , c ⋅ 2,3 , 1 = 0

2 a + 3 b + c = 0

Portanto n → é qualquer vetor cujas coordenadas satisfazem a equação acima. Um vetor possível é

n → = 1 , - 1,1

Passo 4

Então a equação do plano N fica:

n → = a , b . c = ( 1 , - 1,1 )

P 0 = x 0 , y 0 , z 0 = ( 0,0 , 0 )

a x - x 0 + b y - y 0 + c z - z 0 = 0

1 x - 0 - 1 y - 0 + 1 z - 0 = 0

x - y + z = 0

Resposta

A equação do plano é:

x - y + z = 0

Exercícios de Livros Relacionados

Coloque a equação na forma padrão, classifique a superfície e esboce-a. y 2 = x 2 + 1 9 z 2
Determine uma equação da superfície constituída de todos os pontos P para os quais a distância de P ao eixo x é o dobro da distância de P ao plano y z . Identifique a superfície.
Nos exercícios 1 a 6 , esboce o gráfico da superfície de equação dada. 2 x + y + 5 z - 1 0 = 0 .
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. 16 x 2 = y 2 + 4 z 2
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. x 2 + 4 z 2 - y = 0