Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 63
Use a geometria ou simetria, ou ambas, para calcular a integral dupla
Passo 1
E aí, galera! Cês tão bem?
A questão quer que a gente calcule a integral dupla:
Cujo o domínio é a região descrita por:
Este tipo de questão é interessante pois nos cobra o uso de propriedades (quando falamos de simetria estamos pensando na paridade de funções) ou na comparação do sólido com o volume de uma figura.
A estratégia aqui para resolvermos essa questão é que a gente esboce nossa região e entenda onde temos simetria nessa região. Com a ajuda desse esboço já definimos nossos limites de integração.
A forma de calcularmos a integral com simetria nos intervalos muda se estamos integrando uma função par ou ímpar:
- Uma função é par quando
- Já uma função ímpar é aquela em que
Desta forma, uma função par integrada em intervalo simétrico é igual a duas vezes o valor da integral de 0 até o limite do intervalo, isto é,
Quando integramos uma função ímpar em um intervalo simétrico, o resultado final é 0, isto é,
Então vamos resolver nossa integral com base nesses conceitos.
Vem comigo!
Passo 2
Vamos começar por entender a nossa região D e definir nossos limites de integração. Ela é dada entre as curvas
e
Esta última é a parte superior de um círculo. Logo, temos:
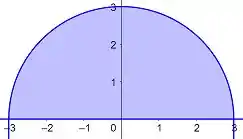
Logo, é uma região simétrica em torno do eixo , com variando de até . Portanto, a nossa integral é:
Pelas propriedades da integral, podemos separar uma integral da soma como a soma de integrais:
Passo 3
Como pode ser visto no passo 1, separamos a integral em duas integrais. Vamos analisar cada uma separadamente. Começando pela primeira, temos:
Como a função é uma função ímpar, isto é, , ao integrarmos em um intervalo simétrico, que é o caso do nosso semicírculo (simétrico em relação ao eixo ) o seu valor é igual a 0! Logo,
Passo 4
Agora, só nos falta resolvermos a segunda parte da integral. E a mesma corresponde a uma integral da unidade. Isto é:
Logo, como a região D corresponde a um semicírculo de raio 3, a sua área é:
Como aqui nosso raio é igual a 3, temos:
Portanto,