Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.5 - Ex. 76
Use um gráfico para dar uma estimativa da área da região que está sob a curva dada. A seguir, encontre a área exata.
,
Passo 1
Oi meus queridos! Vamos que vamos?
A questão pede para estimarmos a área sob a curva usando um gráfico e depois para calcularmos a mesma área usando integral.
A curva que temos é:
,
Usando um software gráfico para desenhar o esboço da região, temos o seguinte:
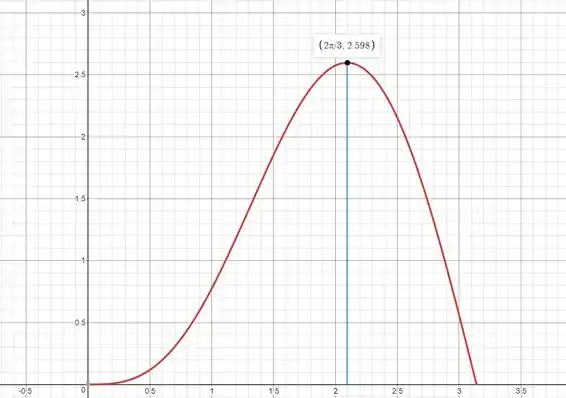
Podemos aproximar a área por um triângulo de base e altura . Assim,
Passo 2
Agora vamos calcular a integral para obter o valor exato:
Podemos abrir a subtração em duas integrais:
Assim, resolvendo primeiro a primeira que é mais fácil temos:
Passo 3
Para segunda integral, vamos usar uma técnica da substituição.
Repara que se usarmos
Nós teremos um seno de um único fator, o que facilita sua integração e além disso a derivada de seria
Que não depende de e isso é importante para escrevermos tudo em função de após a substituição.
Para a técnica da substituição temos que encontrar a diferencial de fazendo:
Dessa forma temos:
E logo,
Por fim, com relação aos limites de integração, também podemos substitui-los. Quando
E quando:
Sendo assim, nossa expressão vai ficar:
A integral de seno de a é zero pois o cosseno terá o mesmo valor nos dois limites de integração.
(Você já pode ficar ligado, a integral do seno em um período completo de vale sempre zero!)
Dessa forma, teremos:
Passo 4
Nossa estimativa foi e o valor exato foi .