Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.5 - Ex. 1
Use os guias desta seção para traçar a curva.
Passo 1
A questão pede para usarmos a roteiro apresentado na seção do livro para fazer um esboço da curva.
Assim, precisaremos encontrar:
O domínio da função, que são os valores que o pode assumir.
As interseções com eixos, que são os valores de quando e de quando .
Limites no infinito, onde faremos:
Intervalos de crescimento e os pontos críticos, onde analisaremos o sinal da derivada da função, fazendo:
Fazer um estuda da concavidade
E qualquer outra consideração que ajude a entender bem o comportamento da função.
Então vem ver tudo isso.
Passo 2
Vamos começar procurando o domínio da função, que são os valores que o pode assumir.
Perceba que sendo nossa função dada por:
Essa é uma função polinomial, logo seu domínio são todos os números reais. Assim:
Passo 3
Para encontrar as interseções com eixos, vamos procurar os valores de quando e de quando .
Assim, no eixo , teremos:
E no eixo , teremos:
Fatorando a equação ficamos com:
Logo, as raízes são e -.
Assim, as interseções são os pontos:
Passo 4
Vamos verificar a existência de simetria, lembrando que:
Testando:
Como é polinomial, ela não é periódica.
Portanto, não há simetria.
Passo 5
Temos que verificar também a existência de assíntotas, mas como nossa função é polinomial não precisamos nos preocupar com isso. Não há assíntotas.
Passo 6
Agora é a hora de olharmos para intervalos de crescimento e decrescimento. Para isso temos que analisar a primeira derivada da função, onde:
Vamos lá, como nossa função é:
Sua derivada será dada pela regra do expoente
Crescente:
Decrescente:
Passo 7
Para encontramos pontos de máximo e mínimo temos que conhecer as raízes de e avaliar se há troca de sinal de Ou então avaliar o sinal da segunda derivada nas raízes de
Vamos lá:
Nas raízes de
Voltando na equação original de
Passo 8
Para analisar a concavidade da função e achar seus intervalos, devemos usar a segunda derivada da função.
Pontos de inflexão ocorrem na mudança de concavidade, isto é quando f’’(x) for igual a zero.
Logo, os intervalos são:
Passo 9
Finalmente podemos esboçar a curva! Vamos fazer um breve resuminho de tudo que descobrimos sobre ela:
;
A curva intercepta os eixos em e ;
Não temos simetria;
Não temos assíntotas;
Intervalo de crescimento: , Intervalo de decrescimento: ;
Ponto máximo , ponto mínimo ;
Concavidade pra cima: ; concavidade pra baixo: , ponto de inflexão:
Desenhando:
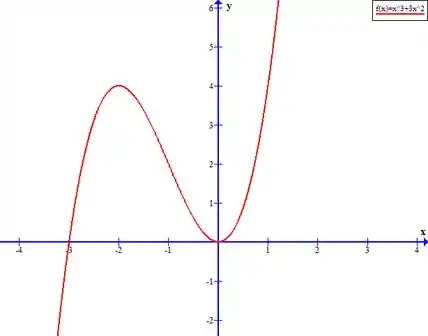
Resposta
