Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 21

Use a integral tripla para determinar o volume do sólido dado.

O sólido delimitado pelo cilindro y = x 2 e pelos planos z = 0 e y + z = 1

Passo 1

Para calcular o volume, vamos calcular a integral

V = ∭ E 1   d V

Podemos achar de cara a variação de z isolando ele na equação do plano y + z = 1

z = 1 - y

E temos a variação 0 ≤ z ≤ 1 - y . Para as outras duas variáveis, vamos ter que analizar y = x 2 e a intersecção do plano y + z = 1 com z = 0 .

Então, repare que, no plano x y :

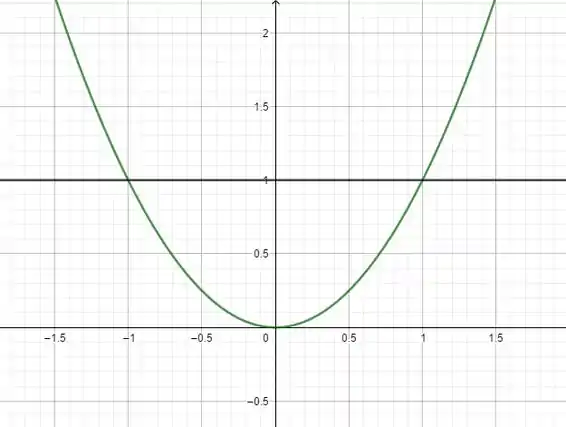
Então a variação de x vai ser - 1 ≤ x ≤ 1 e a de y , o intervalo é x 2 ≤ y ≤ 1 .

Passo 2

Calculando a integral temos

V = ∭ E 1   d V = ∫ - 1 1 ∫ x 2 1 ∫ 0 1 - y 1   d z d y d x

= ∫ - 1 1 ∫ x 2 1 1 - y d y d x = ∫ - 1 1 y - y 2 2 x 2 1 d x

= ∫ - 1 1 1 - 1 2 - x 2 - x 4 2 d x = ∫ - 1 1 1 2 - x 2 + x 4 2 d x

= x 2 - x 3 3 + x 5 10 - 1 1 = 2 1 2 - 1 3 + 1 10

= 2 15 - 10 + 3 30 = 8 15

Resposta

= 8 15

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral tripla.
Calcule a integral iterada. ∫ ∫ ∫ ε x 2 ⋅ e y⋅ d V , onde E é limitado pelo cilindro parabólico z = 1 - y 2 e pelos planos z = 0 , x = 1 e x = - 1 .
Calcule a integral iterada. ∫ ∫ ∫ ε x ⋅ z⋅ d V , onde E é o sólido tetraedro com vértices (0,0,0), (0,1,0), (1,1,0) e (0,1,1).
Calcule a integral iterada. ∫ ∫ ∫ ε x ⋅ y⋅ d V , onde E é o sólido tetraedro com vértices (0,0,0), (1,0,0), (0,2,0) e (0,0,3).
Calcule a integral tripla ∭ E x + 2 y d V , onde E é limitado pelo cilindro parabólico y = x 2 e pelos planos x = z , x = y e z = 0 .