Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.6 - Ex. 16
- Use a Regra do Ponto Médio para as integrais duplas com para estimar a área da superfície , ,
- Use um sistema de computação algébrica para aproximar a área da superfície da parte (a) com precisão de quatro casas decimais. Compare com sua resposta para a parte (a).
Passo 1
Faala, pessoal!
Essa questão pede duas coisas:
Primeiro, temos que usar a regra do ponto médio pra estimar a área de uma superfície.
Depois, vamos calcular a integral usando um software, e comparar os dois resultados.
Pra fazer isso, a gente vai precisar lembrar da fórmula da área de uma superfície definida por em um domínio :
A regra do ponto médio é uma forma de usarmos a soma de Riemann:
Onde os pontos amostrais são os pontos médios de cada partição do domínio .
Passo 2
A função que define a superfície é:
Então calculamos as derivadas parciais, primeiro em função de , com constante:
E em função de , com constante:
Colocando na integral:
Passo 3
(a)
Agora vamos olhar para o nosso domínio e fazer as partições.
O domínio é um retângulo:
E vamos ter partições em e em :
Então fica assim:
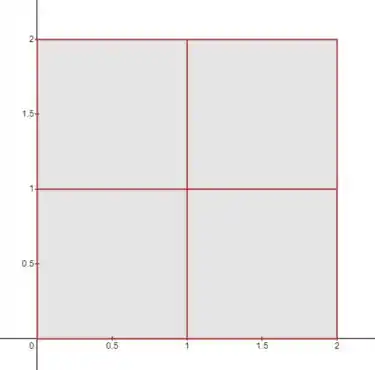
Cada partição é um quadrado de lado . Então o , que é a área da partição, é calculada assim:
Pela regra do ponto médio, nós vamos pegar o ponto no centro de cada partição como ponto amostral:
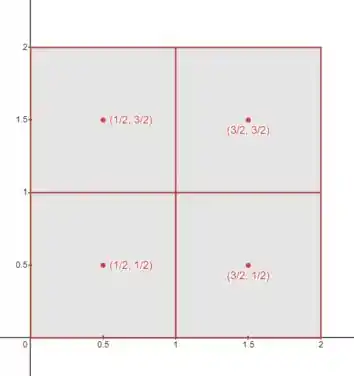
Vamos calcular a soma de Riemann:
Onde .
Como é constante e vale , essa soma fica:
Então precisamos calcular o valor de nos quatro pontos centrais das partições.
No ponto :
No ponto :
No ponto :
E finalmente no ponto :
Voltando pra soma de Riemann:
Então:
Passo 4
(b)
Vamos usar o WolframAlpha pra estimar o valor da integral
Como nosso domínio é retangular:
A integral iterada fica
Calculando no WolframAlpha:
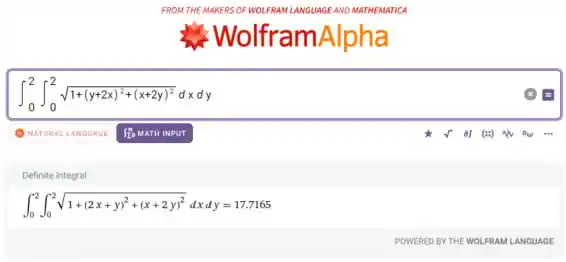
Ou seja,
Vemos que é uma aproximação numérica muito boa em comparação com o cálculo feito por um software. O erro está na primeira casa decimal.