Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.6 - Ex. 15
- Use a Regra do Ponto Médio para as integrais duplas (veja a Seção 15.1) com quatro quadrados para estimar a área da superfície da porção do paraboloide que está acima do quadrado .
- Use um sistema de computação algébrica para aproximar a área da superfície da parte (a) com precisão de quatro casas decimais. Compare com sua resposta para a parte (a).
Passo 1
Oii, tudo bem?? Vamos ver essa questão juntos?
Ela ta pedindo pra gente estimar a área de uma superfície em um domínio . Essa área é calculada pela integral
Na letra (a), a gente vai calcular essa integral pela soma de Riemann:
Usando a regra do ponto médio – ou seja, os pontos amostrais serão os pontos médios de cada uma das partições do domínio.
Depois, na letra (b), vamos transformar essa integral em uma integral iterada, e usar um software (vou usar o WolframAlpha) pra calcular a integral, e comparar com quanto acharmos na (a).
Passo 2
Antes de mais nada, vamos pra equação da nossa superfície:
A função que vamos usar na integral é
Então, vamos calcular as derivadas parciais.
Em função de , considerando constante:
E em função de , com constante:
Colocando na fórmula:
Abrindo os quadrados:
Passo 3
(a)
Agora vamos ver nosso domínio, que é um quadrado
Que foi partido em quadrados (na soma de Riemann, usamos ):
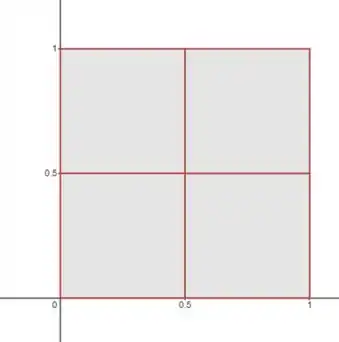
Cada partição é um quadrado, e o lado é . A área disso fica:
Como estamos usando a regra do ponto médio, vamos pegar o ponto no centro de cada partição:
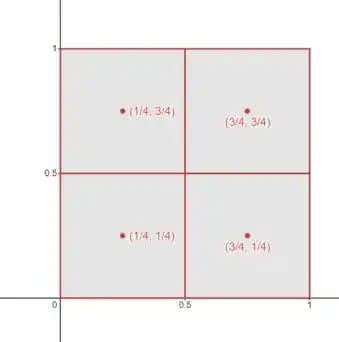
E calcular a soma de Riemann:
Onde .
Só que o é o mesmo pra todas as partições, então ele pode sair do somatório:
Beleza! Agora a gente precisa calcular o valor de nos nossos quatro pontos amostrais, que são os que tão marcados no centro de cada partição.
No ponto :
No ponto :
No ponto :
No ponto :
Então a soma de Riemann:
Ou seja,
Passo 4
(b)
Agora a gente vai ver a integral:
O nosso domínio é um quadrado , então a integral iterada fica:
Vamos jogar isso no WolframAlpha pra estimar o valor:
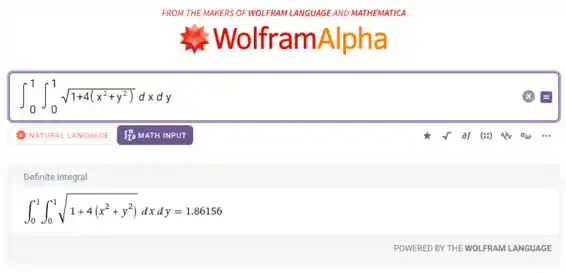
Então,
Vemos que a soma de Riemann é uma aproximação numérica muito boa em comparação com o cálculo feito por um software. O erro está na segunda casa decimal.