Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.6 - Ex. 19

Determine, com precisão de quatro casas decimais, a área da parte da superfície z = 1 + x 2 y 2 que está acima do disco x 2 + y 2 ≤ 1 .

Passo 1

Faala, pessoal!

Essa questão ta pedindo pra gente calcular a área de uma superfície (vamos chamar de S ), em um domínio (vamos chamar de D ).

A fórmula pra isso é:

A S = ∬ D 1 + f x 2 + f y 2 d A

A função f x , y , define a superfície S pelo gráfico z = f x , y

Agora vamos ver o que a gente precisa fazer pra calcular isso?

  1. Encontrar quem é nosso f , e calcular as derivadas parciais
  2. Definir o nosso domínio, e transformar a integral em uma integral iterada
  3. Usar um software (no caso vai ser o WolframAlpha) pra determinar o valor exato dessa integral com precisão de quatro casas decimais.

Vamos lá?

Passo 2

A função que define nossa superfície é:

f x , y = z = 1 + x 2 y 2

Vamos calcular as derivadas parciais.

Quando derivamos em função de x , consideramos y constante:

f x = ∂ 1 + x 2 y 2 ∂ x = 2 x y 2

Derivando em função de y , com x constante:

f y = ∂ 1 + x 2 y 2 ∂ y = 2 x 2 y

Então nossa integral fica assim:

A S = ∬ D 1 + f x 2 + f y 2   d A

= ∬ D 1 + 2 x y 2 2 + 2 x 2 y 2   d A

Abrindo os quadrados:

A S = ∬ D 1 + 4 x 2 y 4 + 4 x 4 y 2   d A

Passo 3

Olhando para o domínio D , ele é definido por:

x 2 + y 2 ≤ 1

Isso é um círculo no plano x y :

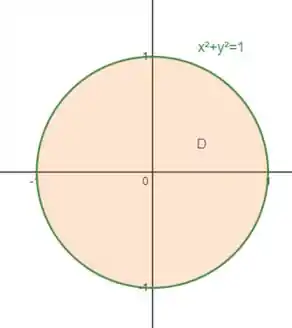
Ele é limitado pela curva x 2 + y 2 = 1 , que podemos reescrever assim:

y 2 = 1 - x 2

⇒ y = 1 - x 2 y = - 1 - x 2

Com o sinal positivo, isso representa a parte de cima da curva ( y ≥ 0 )

Com o sinal negativa, a parte de baixo ( y ≤ 0 )

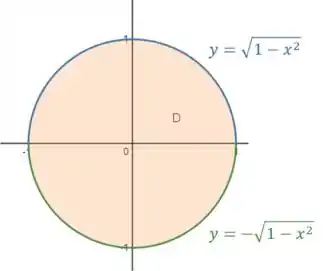
Então, nesse domínio temos:

- 1 ≤ x ≤ 1

- 1 - x 2 ≤ y ≤ 1 - x 2

A integral iterada fica assim:

A S = ∫ - 1 1 ∫ - 1 - x 2 1 - x 2 1 + 4 x 2 y 4 + 4 x 4 y 2 d y d x

Pra calcular, vamos jogar no WolframAlpha:

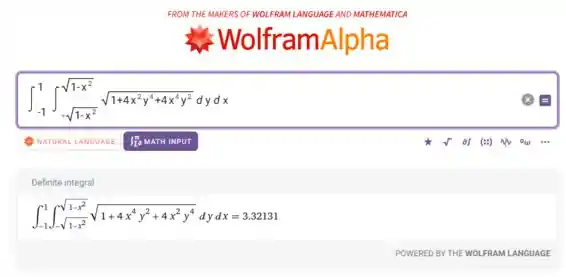
Ou seja,

A S ≈ 3 , 3213

Resposta

A S ≈ 3 , 3213

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é a região triangular delimitada pelas retas x = 0,y = x e 2 x + y = 6 ; ρ x ,y = x 2
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é delimitada por y = e x,y = 0,x = 0 e x = 1 ; ρ x ,y = y
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é delimitada por y = x,y = 0 e x = 1 ; ρ x ,y = x
A função densidade conjunta para um par de variáveis aleatórias X e Y é f x ,y = C x ( 1 + y ) , s e0 ≤ x ≤ 1,0 ≤ y ≤ 2 0 , c a s oc o n t r á r i o á (a) Determine a constante C .(b) Determine P X ≤
Uma lâmina ocupa a região dentro do círculo x 2 + y 2 = 2 y mas fora do círculo x 2 + y 2 = 1 . Encontre o centro de massa se a densidade em qualquer ponto for inversamente proporcional à sua distânci