Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 35
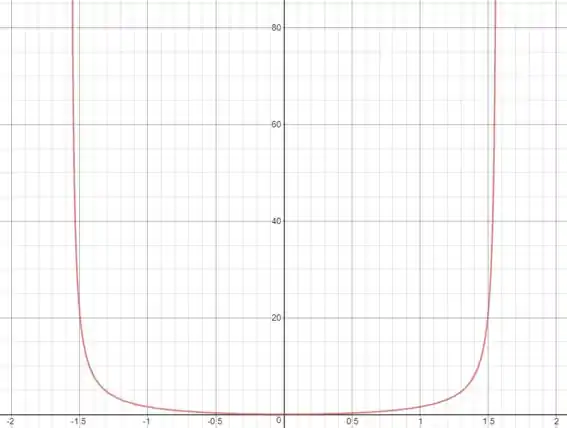
Use o roteiro dessa seção para esboçar a curva.
,
Passo 1
Fala aí, Rafha do Responde aí aqui! Vim te ajudar a matar essa questão...
Temos a seguinte questão:
Definida no intervalo
E aqui vamos seguir o seguinte roteiro para esboçar o gráfico dela.
A. Encontrar o domínio em que a função é definida.
B. Encontrar os interceptos. Que são os pontos onde a função cruza o eixo , isso é:
E o pontos onde a função cruza o eixo , isso é:
C. Verificar se há simetria par, isso é:
Para isso, basta substituir por e verificar se a expressão se mantém a mesma.
Verificar se há simetria ímpar, isso ��:
D. Procurar por assíntotas horizontais e verticais.
Uma assíntota horizontal é um valor real para o qual a função tende quando tende para infinito:
Já uma assíntota vertical é um valor de no qual a função possui uma descontinuidade e tende para infinito.
E. Encontrar os intervalos de crescimento e decrescimento. Para isso, basta derivar a função e nos intervalos em que a derivada for positiva a função cresce
E nos intervalos em que a derivada for negativa a função decresce
F. Encontrar os pontos de máximo e mínimo local.
Esses pontos ocorrem quando a derivada vale zero e troca de sinal ou quando a derivada possui uma descontinuidade e troca de sinal.
Caso a derivada fosse negativa e depois do ponto ela é positiva, então a função possui um ponto de mínimo local. Se a derivada era positiva e depois do ponto ela é negativa, então a função possui um ponto de máximo local.
G. Encontrar os intervalos de concavidade e pontos de inflexão.
A concavidade é para cima se a derivada segunda for positiva
E a concavidade é para baixo se a derivada segunda for negativa
Por fim, um ponto de inflexão é um ponto onde a derivada segunda vale zero e troca de sinal.
H. Esboçar a função juntando as informações obtidas.
Passo 2
O próprio exercício delimitou o limite que devemos considerar:
Passo 3
A função é ímpar
Assim como a tangente
Como o produto de uma função ímpar por outra função ímpar é par, segue que a função é par.
Desta forma, ela é simétrica com relação ao eixo e só precisamos nos preocupar com .
Passo 4
Para encontrar o intercepto fazemos:
no intervalo a tangente não se anula em nenhum ponto além de .
Esse é o único intercepto pois a função não se anula em mais nenhum ponto dentro do intervalo dado.
Como a curva passa pela origem , temos que o intercepto ocorre em .
Passo 5
Como estamos trabalhando num intervalo limitado, não faz sentido fazer limites no infinito para procurar assíntotas horizontais.
Todavia, sabemos que a tangente explode em , de modo que podemos tomar esse limite para ver o que acontece:
Como a função é par, para ocorre o mesmo
De modo que as retas e são assíntotas verticais da curva.
Passo 6
Vamos estudar agora o crescimento e decrescimento da curva fazendo a derivada da função:
Aplicando a regra do produto, temos:
Sabemos que pois esse fator está elevado ao quadrado.
E que no primeiro quadrante (isso é, para ), tanto como são positivos, de modo que
Já no quarto quadrante (isso é, para ), tanto como são negativos, de modo que
Assim, a função é decrescente para e crescente para .
Passo 7
Para a concavidade usaremos a segunda derivada:
Podemos colocar em evidência:
Vimos no passo 6 que e têm sempre o mesmo sinal, de modo que .
Portanto o fator sempre será positivo.
O fator também é sempre positivo, pois a secante está elevado ao quadrado.
Assim, vemos que
e a concavidade da curva é sempre para cima e portanto não há pontos de inflexão.
Passo 8
Com esses dados podemos fazer o esboço da nossa curva:
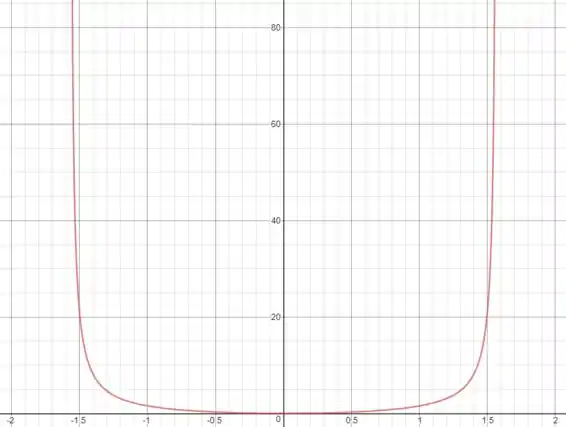
Resposta
Assim, o gráfico da função será algo do tipo
