Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.5 - Ex. 38
Use o roteiro desta seção para esboçar a curva
Passo 1
Pra começar, vamos encontrar o domínio da função.
Repare que não temos nenhuma restrição. Assim, o domínio da nossa função será .
Passo 2
Agora vamos ver os pontos de interseção com o eixo .
Se :
Passo 3
Para analisarmos a simetria. É importante vermos se nossa função é ímpar ou par. Então vem comigo:
Vamos ver como fica o :
Como o seno é uma função ímpar:
Com isso, vemos que . Portanto, nossa função será ímpar o que nos leva a concluir que a curva será simétrica com relação ao eixo .
Passo 4
Seguindo o roteiro, chegamos à tarefa de analisar as assíntotas.
- Assíntota horizontal:
Como a função seno é limita entre , quando o termo irá superar a função seno. Logo,
Para :
Assim,
Então, vemos que não teremos nenhuma assíntota horizontal.
Passo 5
Para acharmos os intervalos de crescimento e decrescimento, temos que achar .
Derivando,
Para :
Logo, não há solução nesse caso, pois nunca pode ser maior que 1.
Para :
Resolvendo a inequação:
, com .
Logo, nossa função será decrescente no intervalo acima.
Passo 6
Agora temos que achar os valores máximo e mínimos. Para isso, vamos fazer :
Logo,
Resolvendo, temos:
, com
Passo 7
Para terminar, basta analisarmos as concavidades da curva. Para isso, vamos ver o sinal de .
Derivando,
Para :
Logo,
Resolvendo, temos:
Nesse intervalo, nossa curva possui concavidade para cima.
Para :
Logo,
Resolvendo, temos:
Nesse intervalo, nossa curva possui concavidade para baixo.
Passo 8
Pra finalizar, basta esboçarmos o gráfico de :
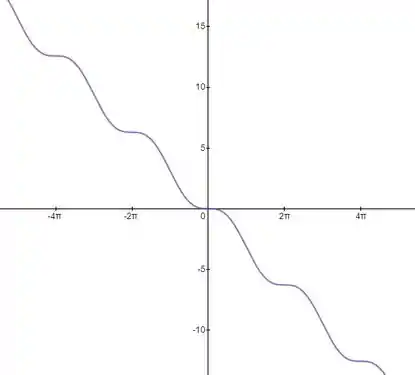
Resposta
Ei, a resposta está no passo a passo :)