Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 38
Use um sistema de computação algébrica para achar o volume exato do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno da reta especificada.
Passo 1
Bom galera, antes de começar vamos lembrar como se calcula o volume de um sólido de rotação:
Vamos desenhar a figura do sólido, ok?
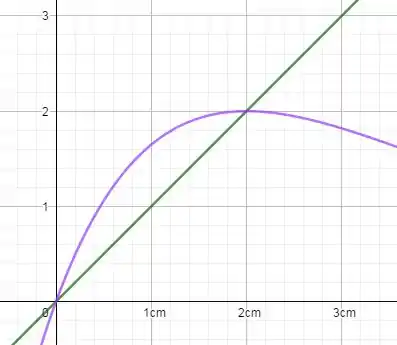
Primeiro vamos calcular a área da secção transversal. Mas como?
Esta área será a área da reta até a função menos a reta até a função
E não vamos esquecer do Então:
Reorganizando:
Passo 2
Antes de jogarmos no volume precisamos dos limites de integração, os ponto onde as funções se encontram:
Então:
Vamos aplicar ln em ambos os lados:
Já sabemos nosso intervalo de integração, já que o x vai de
Já descobrimos o volume, agora é só aplicar em um sistema de computação algébrica: