Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.9 - Ex. 34

Utilize coordenadas esféricas.

Determine a massa e centro de massa do hemisfério sólido de raio a se a densidade em qualquer ponto for proporcional à sua distância da base.

Passo 1

Vamos lá pessoal tudo certo? Veja que essa questão é um pouco diferente, temos que calcular a massa e centro de massa de um hemisfério sólido. Porém, a densidade não é constante. Na verdade, a densidade varia de acordo com a distância da base.

A equação da massa:

m = ∭ D δ   d V

E do centro de massa em relação a uma coordenada r qualquer

r - = 1 m ∭ D r δ   d V ,

Ambos apresentam o termo referente a densidade. Por isso deve ser a primeira coisa a ser descrita matematicamente.

Passo 2

Como vamos estudar um hemisfério, vamos usar a esfera x 2 + y 2 + z 2 = a 2 , com z ≥ 0 . Assim, a base do hemisfério está no plano x y e a distância de um ponto x , y , z até essa base vai ser

d = z

Portanto, a densidade será

δ = k z

Perceba que poderíamos ter criado esse hemisfério em qualquer eixo. Escolhemos o eixo z por comodidade, por ser uma figura circular, tudo lhe é simétrico com exceção ao eixo de sua altura, veja:

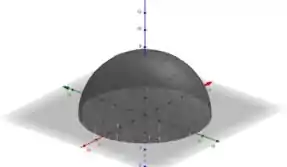
Devido a simetria, temos que as coordenadas x e y do centro de massa se anulam. Já para z :

z - = 1 m ∭ D z δ   d V ,

onde m é a massa

m = ∭ D δ   d V

Como z ≥ 0 , em coordenadas esféricas teremos 0 ≤ ϕ ≤ π / 2 . Assim,

m = k ∫ 0 2 π ∫ 0 π 2 ∫ 0 a ρ cos ⁡ ϕ ⋅ ρ 2   s e n   ϕ   d ρ   d ϕ   d θ

z - = k m ∫ 0 2 π ∫ 0 π 2 ∫ 0 a ρ 2 cos 2 ⁡ ϕ ⋅ ρ 2   s e n   ϕ   d ρ   d ϕ   d θ

Passo 3

Para achar a massa, temos

m = 2 π k   ∫ 0 a ρ 3 d ρ ∫ 0 π 2 cos ⁡ ϕ   s e n   ϕ   d ϕ

Assim,

m = 2 π k p 4 4 0 a sen 2 ⁡ x 2   0 π 2        

m = 2 π k ⋅ a 4 4 ⋅ 1 2 = π k   a 4 4

Passo 4

Já para o centro de massa

z - = 2 π k m ∫ 0 a ρ 4 d ρ ∫ 0 π 2 cos 2 ⁡ ϕ   s e n   ϕ   d ϕ

Assim,

z - = 2 π k m ⋅ a 5 5 ⋅ 1 3 = 2 π k a 5 15 ⋅ 1 m

Usando a expressão para massa que encontramos:

z - = 2 π k a 5 15 ⋅ 4 π k   a 4 = 8 a 15

( 0,0 , 8 15 )  

Resposta

m = π k   a 4 4     e     ( 0 ,   0 , 8 a 15 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Centro de massa e momento de inercia: repita o exercício 19 para δ x , y = 3 x 2 + 1
Encontrando o centro de massa: encontre o centro de massa de uma placa triangular fina delimitada pelo eixo y e as retas y = x e y = 2 - x se δ x , y = 6 x + 3 y + 3
Encontrando um centro de massa e momento de inércia: encontre o centro de massa e o momento de inercia em relação ao eixo y de uma placa retangular fina cortada no primeiro quadrante pelas retas x = 6
Encontrando o momento de inercia: encontre o momento de inercia em relação ao eixo x de uma placa fina de densidade δ = 1 delimitada pela circunferência x 2 + y 2 = 4 . Em seguida, utilize seu resulta
Encontrando a massa: encontre a massa de uma placa fina ocupando a região menor cortada pela elipse x 2 + 4 y 2 = 12 pela parábola x = 4 y 2 se δ x , y = 5 x