Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.1 - Ex. 26
- Utilize a Definição 2 para achar uma expressão para a área sob a curva de a como um limite.
- A fórmula a seguir para a soma dos cubos dos primeiros inteiros está demonstrada no Apêndice E. Use-a para calcular o limite da parte (a).
Passo 1
Eaee! Bora pra mais uma questão?!
Bom... Aqui a gente precisa achar uma expressão para a área sob a curva com de a como um limite, usando a Definição 2.
A Definição 2, que diz que: A área da região S que está sob o gráfico de uma função contínua é o limite da soma das áreas dos retângulos aproximantes:
Vamos ver o esboço dessa curva pra ficar mais palpável:
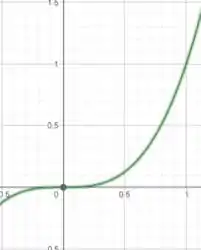
Em outras palavras é como se a gente dividisse a área abaixo dessa curva com retangulinhos infinitos com a espessura muito pequeninha, que tende a .
Com isso podemos desenvolver a fórmula da definição 2 para nossa função e encontrar a área abaixo da curva no intervalo dado.
Bora aplicar?? 😉
Passo 2
Com a função dada podemos achar o seguinte delta a partir do intervalo da região:
Como estamos saindo da origem, nosso é dado por:
Dessa forma:
Portanto:
Usando a definição:
Simplificando:
Show?
Passo 3
Na letra (b) o enunciado pede pra a gente calcular o limite que achamos em , usando a seguinte fórmula:
Onde é um número inteiro. Da letra (a) temos:
Temos que:
Então:
Vamos simplificar pra calcular o limite:
Calculando o limite, temos que:
Prontinho! Entendeu tudo? Responde Aí! 😉