Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 56
Utilize a simetria para calcular , onde é a região delimitada pelo quadrado com vértices e .
Passo 1
Fazendo um esboço da região de integração, obtemos:
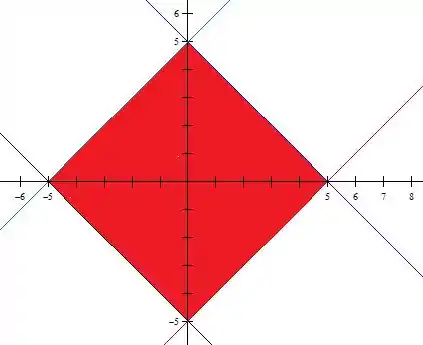
Como a região é simétrica com relação a ambos os eixos, podemos fazer considerações de simetria. Observe que tanto como são funções ímpares com respeito a suas variáveis, de modo que suas integrais em intervalos simétricos devem se anular:
Assim,
Passo 2
A integral que restou é simples de ser calculada: é área do quadrado. O lado do quadrado é calculado usando Pitágoras:
Assim,
Portanto,
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. A sr e t a sy = 2 x,y = x 2ey =
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. a sr e t a sx = 0 ,y = 2 x ,ey =
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. a sc u r v a s y = ln x ey = 2
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. a sr e t a s y = 1 - x ,ey = 2 ,
As integrais e somas de integrais nos Exercícios 13-18 fornecem as áreas das regiões no plano xy. Esboce cada região, marque cada curva limitante com sua equação e forneça as coordenadas dos pontos on