Equação Exponencial
Produzido por Erick PinhoTeoria
Você sabe o que é uma Equação Exponencial?
A Equação Exponencial é uma expressão algébrica que contém pelo menos uma incógnita no expoente.
-Hãam?! 😖
Vou explicar melhor! Quando eu digo expressão algébrica, eu estou querendo dizer que ela tem uma igualdade. Já a incógnita no expoente é nada mais do que um número desconhecido, que geralmente representamos por “
Exemplos de Equações Exponenciais:
Conseguiu pegar o espirito da coisa?!
Hoje a gente vai aprender sobre equações exponencias e logarítmicas! Se liga nesse vídeo super completo, que o Responde Aí preparou pra você, com tudo o que você precisa saber sobre esse assunto 👇👇👇
Propriedades de Potências
Antes de qualquer coisa, vamos fazer uma breve revisão sobre potência e suas propriedades! 😁
A potência tem essa carinha aqui:
Dando nome aos bois, a potência tem a seguinte “anatomia” hahha:
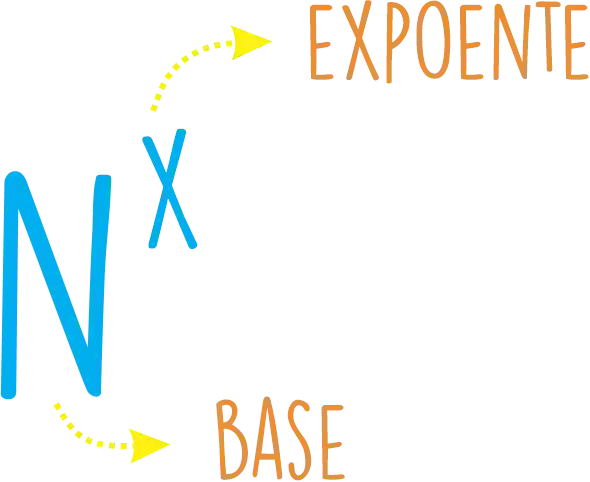
Existem algumas propriedades de potências que são muuuito importantes a gente ter em mente!
Propriedade 1: Potência com expoente igual a zero
Um número qualquer elevado a zero vai ser sempre igual a
Exemplo:
Propriedade 2: Potência com expoente igual a 1
Um número elevado a
Por exemplo:
Propriedade 3: Potência com expoente negativo
Quando temos uma potência de expoente negativo, escrevemos o inverso da base para que o expoente fique positivo. Assim:
Exemplo:
Propriedade 4: Multiplicação de potências com a mesma base
Quando temos duas bases iguais em uma multiplicação, repetimos a base e somamos o expoente:
Exemplo:
Propriedade 5: Divisão de potências com a mesma base
Essa propriedade segue o mesmo raciocínio que a propriedade de multiplicação! Quando temos duas bases iguais em uma divisão, repetimos a base e subtraímos o expoente:
Exemplo:
Propriedade 6: Potência da potência
Quando temos uma potência de potência, conservamos a base e multiplicamos os expoentes. Assim:
Exemplo:
.
Propriedade 7: Potência com expoente fracionário
E pra acabar, quando o expoente da potência é uma fração, escrevemos essa potenciação como uma radiciação. Bem assim:
Exemplo:
Se liga na imagem abaixo, com o resumo de todas essas propriedades de potências super importantes:

Beleza, mas a gente esta interessado em equação exponencial, não é mesmo!? 🤣🤣🤣
Passo a Passo de Como Resolver uma Equação Exponencial
Vamos dar uma olhada em um exemplo:
Passo 1: Colocar todos os elementos na mesma base
Sabemos que:
Então podemos substituir na equação:
Passo 2: “Cortar” a base e igualar os expoentes:
Passo 3: Resolver a equação algébrica
Mas essa estava fácil! Vamos fazer um exercício envolvendo fração exponencial!
Exercício Resolvido: Equação Exponencial com Fração
Resolva a seguinte equação exponencial:
Uhhhh, e agora?!! 😱
Vamos organizar os pensamentos! Temos
Então vamos tentar colocar o
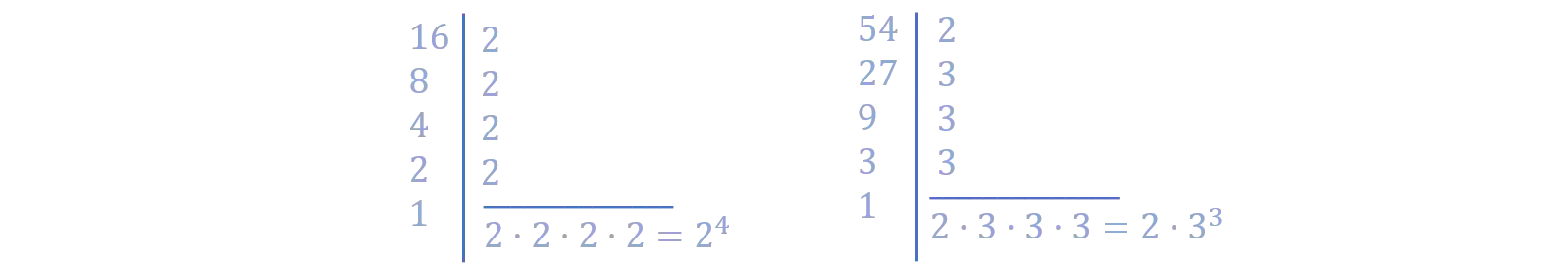
Agora a gente pode reescrever a equação:
Opaa, agora ficou fácil heim!
Mas repara que o numerador e o denominador estão ao contrário! Para resolver esse problema, podemos fazer o seguinte:
Tá vendo porque que é importante ter as propriedades na ponta da língua?! Agora estamos de cara pro gol, é só finalizar!
Aweeee!
O logaritmo
Agora vamos entender um pouco mais de Logaritmo! O logaritmo está intimamente ligado a exponencial. Ele tem essa carinha aqui:
Ou um exemplo numérico:
Ele remete a seguinte pergunta: 10 (base) elevado a qual número tem como resultado
A resposta para essa pergunta é
Essa base
Quando você ver um log com base oculta, lembre-se que é base . Outras bases estarão especificadas!
Assim como as potências, aqui é muito importante estar atento em algumas propriedades! Você pode conferir as propriedades de
O logaritmo natural
Assim como a base
Essa base, assim como a base
Onde o
Equação Logarítmica
A partir disso tudo, podemos falar das equações logarítmicas. Para resolver, a ideia é colocar tudo na mesma base ou tentar cotar o log usando suas propriedades. Vamos ver como isso fica?
Tá, mas qual como transformar esse zero num log de base ? É simples, só lembrar das propriedades:
Então:
E podemos escrever:
Uma vez que está tudo na mesma base, podemos “cortar” o log:
Essa é a solução do problema:
Ihuuul!! Agora bora praticar com mais exercícios?!