Equação Modular
Produzido por Erick PinhoTeoria
Bora bater um papo sobre Equação Modular com o Responde Aí?!
O que é uma Equação Modular
Uma equação modular é uma equação com pelo menos uma incógnita

O valor de todo módulo é sempre positivo independente do número dentro ser positivo ou negativo.
O que é Módulo?
O módulo é o valor absoluto de um número real! Ou seja, quando o número é positivo, o módulo é exatamente o número. Já quando é negativo, o módulo é igual ao valor positivo do número.
Por exemplo:

Para ser igual a parte positiva quando o argumento é negativo, multiplica-se por
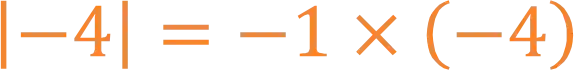
O módulo surge para definir o conceito de distância. A distância não está relacionada com nenhum sentido e não pode ser considerada negativa, por isso o módulo trata de valores positivos. Dessa maneira, o seu valor será o módulo do número ou o seu valor absoluto.
De uma forma geral, podemos dizer que:
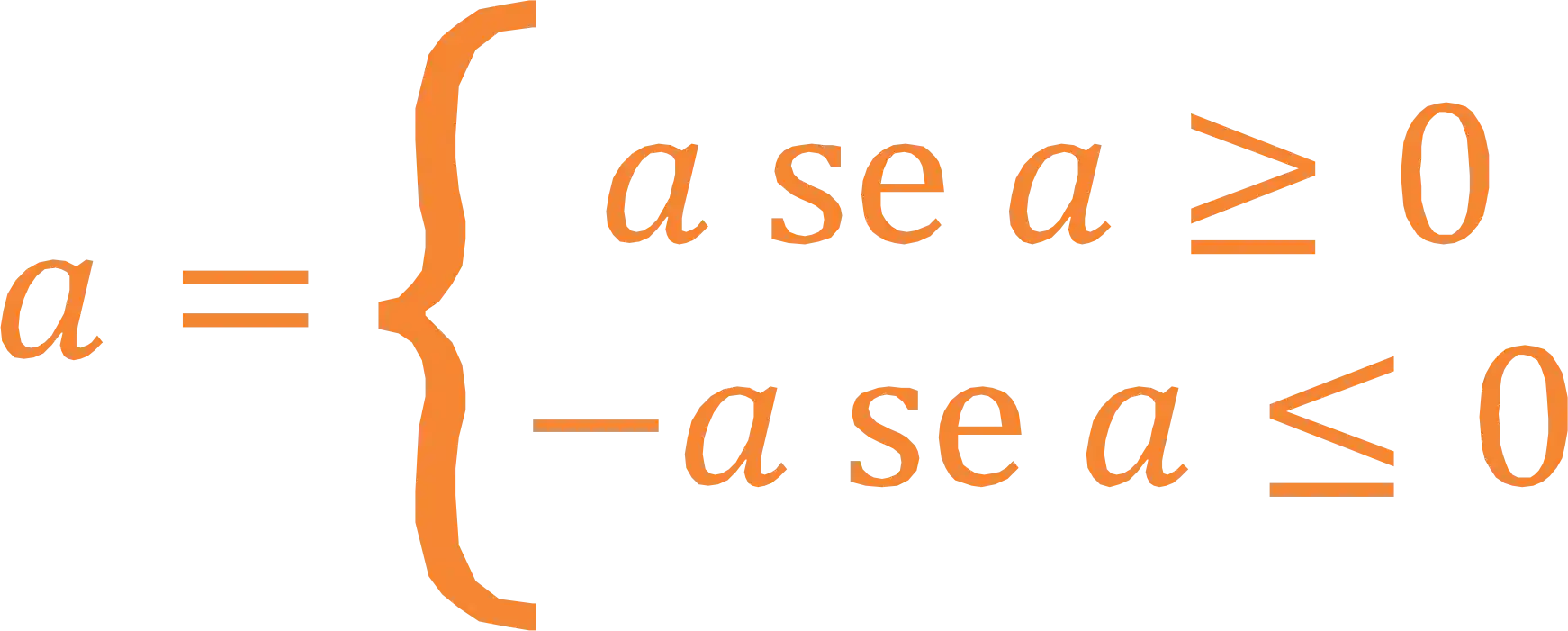
Como Resolver uma Equação Modular
Existem duas formas de resolver uma equação modular, a primeira é pela sua definição e a segunda é um macetezinho que simplifica bastante as coisas!
Bora aprender essas duas formas?!
Agora vamos ver como resolver as equações envolvendo módulo!
Aqui não tem muito mistério, temos uma forma que sempre funciona. Vamos resolver pela definição! Pra isso vamos voltar ao nosso exemplo inicial:
O que é resolver pela definição? É usarmos a definição de módulo para resolver a nossa função!
Fazemos uma análise de sinal:
Agora vamos resolver essa equação para cada intervalo. Começando com
Achando a resposta temos que ver se ela está no intervalo que estamos trabalhando, e está, pois
Agora com
Esse valor está no intervalo que estamos vendo, então a solução vai ser:
Entendeu a ideia? Claro que isso pode ser mais complexo, nos exercícios vamos ver outros casos!
Como Resolver uma Equação Modular: Macete
A outra forma é um pouco mais maceteada mas é sempre fazer a mesma coisa, ela não se preocupa com a definição. Vamos refazer o exemplo com isso:
Agora vamos transformar isso em duas equações diferentes, uma igualando o cara dentro do módulo a
Agora é só olharmos rapidinho se esses valores servem na equação:
Os dois valores valem, e pronto terminamos a nossa conta. Entendeu a lógica?
Primeiro consideramos o valor dentro do módulo como ele mesmo e vemos se o resultado está dentro do intervalo onde isso é verdade. Depois, consideramos o valor dentro do módulo multiplicado por
Vou te mostrar uma intuição geométrica disso! Lembra que eu falei que o módulo fala de distância? Então, se você se deparar com algo assim:
Você tem que pensar quais números perto de

Olha aqui em cima, quais números têm
De uma forma geral, quando você se deparar com:
Você estará pensando nos números que distam r unidades de
Vamos aplicar isso nos exercícios? Vamos lá!
Como Resolver uma Equação Modular: Macete
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Calcule:
Passo 1
Opa! Vamos lá! Antes de mais nada, precisamos entender que módulo é a distância de um ponto da reta à origem:

Então, a distância do ponto até a origem é , concorda?!
a) Utilizando esse raciocínio,
Beleza?!

Passo 2
b) Aqui queremos calcular o , vamos utilizar a mesma idéia da letra (a)? Sim! Da mesma forma, a distância do ponto à origem é , pois não existe distância negativa, concorda?!
Assim,
Beleza?!
c) Da mesma forma, a distância do ponto à origem é . Logo,

d) Pra finalizar, falta calcularmos . Aí eu te pergunto: Qual a distância do ponto à origem??? Isso messsssmo! É zero! Ahahahahah
Beleza?!
Resposta
- 120
- 0
Exercício Resolvido #2
Elaboração Própria
Resolva a equação modular abaixo
Passo 1
Vamos lá!!! Queremos resolver a equação modular
Certo?! Antes de fazer as continhas vamos relembrar a definição de módulo?

A definição de módulo é
Beleza?! É essa idéia que vamos usar para resolver esse exercício!
Passo 2
Assim, usando a definição
Podemos dar uma arrumada e ficaremos com
Beleza?!
Agora vamos resolver essa equação por partes!

Passo 3
Começando quando. Nesse caso, teremos
Para isolar o , basta passarmos o 10 pro lado direito da equação
Assim,
Beleza?!
Agora vamos utilizar o mesmo raciocínio para :
Assim, isolando o :
Portanto,
Assim, nossas respostas são
Show de bola?!
Resposta
Exercício Resolvido #3
Elaboração Própria
Calcule Aí
Passo 1
Epaa! Let’s Go! Para resolver esse exercício, vamos utilizar a definição de módulo:
Beleza?!

Passo 2
Assim, usando a definição
Podemos dar uma arrumada e ficaremos com
Beleza?!
Agora vamos resolver essa equação por partes!

Passo 3
Começando quando. Nesse caso, teremos
Precisamos então isolar o
Fazendo as continhas, temos
Dividindo ambos os lados por
Passo 4
Agora vamos utilizar o mesmo raciocínio para :
Isolando o
Fazendo as contas,
Assim,
Podemos simplifcar por :
Assim, nossas respostas são
Show de bola?!
Resposta
Exercício Resolvido #4
Elaboração Própria
Resolva a equação modular abaixo
Passo 1
Fala Aí!! Para resolver essa questão, vamos utilizar a propriedade abaixo:
Beleza?!

Passo 2
Assim, substituindo na propriedade, temos
Vamos resolver por partes!!
Começando pela equação de cima:
Isolando , temos
Ou seja,
Beleza?!
Passo 3
Agora vamos resolver a segunda linha
Isolando o , temos
Assim,
Dividindo ambos os lados da equação por , temos
Show de bola?!
Portanto, temos como solução
Resposta
Exercício Resolvido #5
PUC-SP
O conjunto solução da equação é:
Passo 1
Vamos laááá!! Como podemos resolver essa questão? Ó, sabemos que o módulo não pode ser negativo. Assim,
Ou seja,

Mas vamos lá! Para resolver esse exercício, vamos utilizar a definição de módulo:
Beleza?!
Passo 2
Assim, usando a definição
Podemos dar uma arrumada e ficaremos com
Beleza?!
Agora vamos resolver essa equação por partes!
Passo 3
Começando quando. Nesse caso, teremos
Precisamos então isolar o
Fazendo as continhas, temos
Passo 4
Agora vamos utilizar o mesmo raciocínio para :
Isolando o
Fazendo as contas,
Assim,
MAS PERAAAA!!!

O conjunto solução seria , mas pela condição inicial,
E os dois valores que encontramos são menores do que . Logo, a solução correta é
Resposta
Letra C
Exercício Resolvido #6
Fundamentos da Matemática Elementar Vol. 2 Gelson Iezzi.
Resolva em as seguintes equações:
Passo 1
Aqui é molezinha. Basta só a gente fazer os estudos dos casos positivos e negativos, para
Vamos ter:
Caso positivo:
Resolvendo a nossa equação do segundo grau, teremos:
Caso negativo:
Resolvendo a equação do segundo grau dessa bagaça, teremos:
Daí...
Resposta
Exercício Resolvido #7
Elaboração Própria
Resolve Aí a seguinte equação em :
Passo 1
Vamos analisar os dois termos com módulo separadamente:
Passo 2
Beleza, então vamos reescrever essa equação em três intervalos diferentes:
No intervalo , temos:
Então a equação fica:
Essa é uma das soluções da equação!
Passo 3
No intervalo :
A equação é:
Show, achamos mais uma solução.
Passo 4
Agora o último intervalo, , onde
Então a equação é
Achamos a mesma resposta que antes, então esse intervalo não agregou nada novo.
Portanto, a equação tem só duas soluções mesmo: e .
Resposta
Exercício Resolvido #8
UVA - Adriana Tostes - Lista 4 - 1l
Resolva em as equações:
Passo 1
Como o lado esquerdo tá dentro do módulo, vamos dividir a equação em duas, uma para qual:
E outra em que:
Passo 2
Para a primeira, temos:
Logo, as raízes serão:
Mas pra esses valores serem raiz, a gente tem que ver se eles batem com a condição inicial! A primeira, no caso, em que:
Então pro valor ser raiz, quando a gente substituir na equação temos que achar um valor positivo.
Vamos ver se esses valores batem com a condição:
Para :
Como e nessa raiz, temos:
O que viola a condição imposta e, portanto, não é raiz!
Vamos testar agora para :
Como e nessa raiz, temos:
Logo, é uma das soluções do problema!
Passo 3
Agora consideramos:
Substituindo:
Que possui raízes:
Para a primeira raiz, temos:
Dessa maneira, para a primeira raiz, temos:
Que segue as condições e será solução do problema. Agora, para a segunda raiz:
Que leva a:
Que viola as condições impostas e não faz parte da solução do problema.
Com isso, o conjunto solução será:
Resposta
Exercício Resolvido #9
Fundamentos da Matemática Elementar Vol. 2 Gelson Iezzi.
Resolva em as seguintes equações:
Passo 1
Vamos dar uma arrumada nessa equação! Passando um dos módulos pro lado direito:
Desta forma:
Opa, mas calma lá! Porque o sinal de não apareceu no lado direito? Não foi mágica nem nada, o que acontece é que é sempre positivo, não importa o valor de que a gente escolha. Chegamos então a 2 casos:
Passo 2
O primeiro caso fica
Os vão sumir, daí vai sobrar só uma equaçãozinha do 1º grau:
Passo 3
O segundo caso fica
E a fórmula de Bhaskara nos dá
Nesse caso, a equação de segundo grau não nos dá raízes reais. Uma pena : (
Resposta
Exercício Resolvido #10
UVA - Adriana Tostes - Lista 4 - 1j
Resolve em as equações:
Passo 1
Como o módulo é sempre positivo, temos que:
Que também sempre será positivo por estar elevado ao quadrado. Assim sendo, podemos reescrever a equação da seguinte forma:
Podemos agora separar essa equação em duas, uma para qual:
E outra para qual:
Vamos fazê-lo.
Passo 2
Para , temos:
Que tem raízes:
Como para valores positivos (), então viola as condições impostas e não é parte da solução, restando, portanto, .
Passo 3
Para , temos:
Que tem raízes:
Como para valores negativos (), então viola as condições impostas e não é parte da solução, restando, portanto, .
Assim sendo, as solução do problema será: