Funções Injetoras, Sobrejetoras, Bijetoras e Inversas
Produzido por Erick PinhoTeoria
Introdução
Quando começamos a falar de funções, aprendemos que para uma variável dependente ser função de uma variável independente é necessário que para cada valor de , só exista um associado, ou seja, numa função o que entra só pode ter um único valor de correspondente.
Essa condição determina a existência da função, mas há também outras condições que servem para classificar as funções em algumas categorias, que são: funções injetoras, sobrejetoras e bijetoras.
Você pode pensar que essas categorias só servem pra inventar mais coisa pra te confundir, mas vamos ver que elas são uma condição para entendermos as funções inversas, que são muito importantes e que veremos mais à frente!
Então, vem comigo e vamos ver direitinho isso aí ;)
Funções injetoras
Repare no gráfico de uma parábola abaixo:
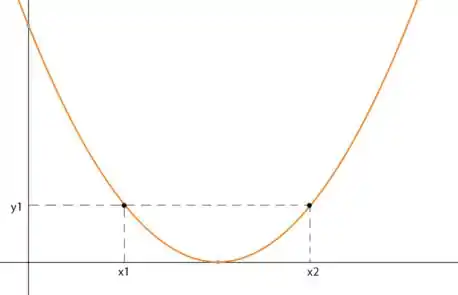
Nessa função, para os pontos diferentes e , temos um mesmo valor de associado:
Agora repare nesse outro:
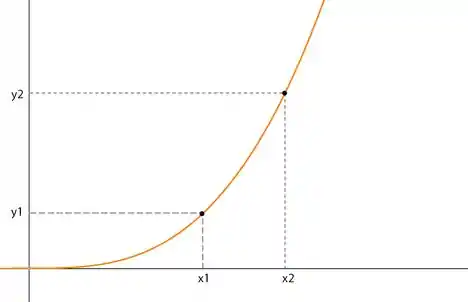
Para quaisquer pontos diferentes e que escolhermos, temos sempre valores diferentes de :
Essa é a definição de uma função injetora! Nesse tipo de função, temos que dois valores diferentes de , sempre resultam em valores de diferentes.
Uma função é injetora se para dois pontos quaisquer pertencentes ao domínio de :
Tivermos:
Função sobrejetora
No gráfico da função abaixo, temos uma parábola:
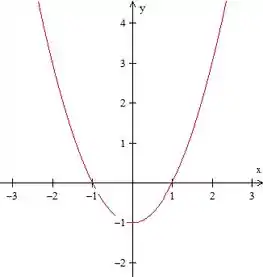
Repare em um detalhe importante desse gráfico: ele possui um ponto extremo, neste caso, um ponto de mínimo quando .
Isso significa que não importa o valor de que escolhermos, teremos sempre que:
A imagem de , que representa o conjunto de todos os resultados obtidos da função, está limitada a todos os números reais maiores ou iguais a :
Mas temos ainda o contradomínio, que é conjunto de todo os valores de que poderíamos obter na função e que não é limitado, continua sendo o conjunto de todos os números reais:
Vamos olhar outro exemplo, uma função cúbica:
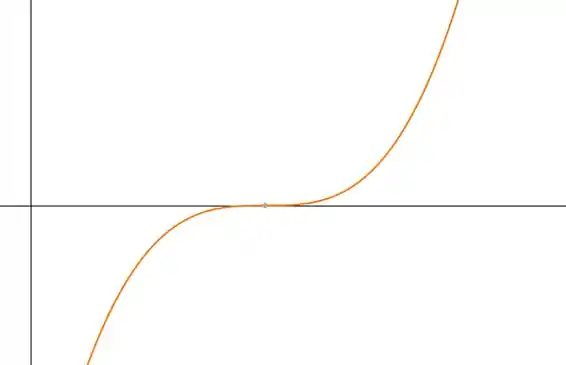
Nela, a função passa por todos os valores de possíveis, ou seja, o conjunto imagem é igual ao contradomínio!
Uma função é sobrejetora se para cada valor de existir ao menos um valor de associado:
sobrejetorasDentro desta definição, a parábola tem, por exemplo não associado a nenhum e, por isso, não é sobrejetora.
Funções bijetoras
Quanto as bijetoras, não há nada de novo a considerar. Chamamos uma função de bijetora se ela for ao mesmo tempo injetora e sobrejetora!
Um exemplo de função desse grupo é a função cúbica:
Função inversa
Imagine que temos a função:
Neste caso, temos uma função, pois cada valor de está associado a um único valor de , ou seja, é uma função de .
Mas e se, ao invés de representarmos como função de , quiséssemos colocarmos como função de ?

Pra isso, precisaríamos isolar :
Se trocarmos por e por simplesmente para manter a notação usual das funções ficamos com:
Essa função não é uma função qualquer, ela é a função inversa de e pode ter a notação:
Com esse sobrescrito .
Então, é basicamente assim que determinamos uma função inversa, isolando e substituindo por e vice-versa ao final.
Infelizmente, nem tudo são flores e nem toda função tem sua inversa. Vamos ver, por exemplo:
Se tentarmos isolar , obtemos não:
Mas sim:
Esse indica que são geradas duas funções, uma positiva (em azul) e outra negativa (em verde).

Isso acontece, pois, para uma função ser invertível, ou seja, para ter uma função inversa, é necessário ser bijetora.
O primeiro exemplo é de uma função bijetora e por isso, possui inversa, enquanto a parábola do segundo exemplo não é nem injetora, nem sobrejetora, como vimos ao longo desse tópico, por isso, não pode ser invertida usando somente uma função.
Isso é necessário porque uma função inversa também é uma função e, portanto, precisa que cada valor de esteja associado a somente um .
E quando isolamos para achar a inversa, colocamos em função de , então um valor precisa estar sempre associado a somente um valor de , o que não acontece na parábola do nosso exemplo, mas é verdade para todas as funções bijetoras.
Funções inversas relevantes
Falaremos aqui de algumas funções inversas mais conhecidas. Se você não viu algumas dessas funções para as quais traremos a inversa, não tem problema. Agora, se as funções são relevantes para seu estudo, fique atento nas suas respectivas inversas!
Uma propriedade muito útil associada as funções inversas é:
Isso significa que uma função com argumento igual a sua inversa tem como resultado o argumento da inversa.
Como, por exemplo:
É como se as funções inversas se anulassem e sobrasse só o que está lá dentro! E isso vale mesmo quando há uma função como argumento da inversa:
Por exemplo:
Shooow?
Função sobrejetora
Funções bijetoras
Função inversa
Funções inversas relevantes
Exercícios Resolvidos
Exercício Resolvido #1
Matemática Elementar – Gelson Iezzi e Carlos Murakami – 3ª edição – Pág. 191
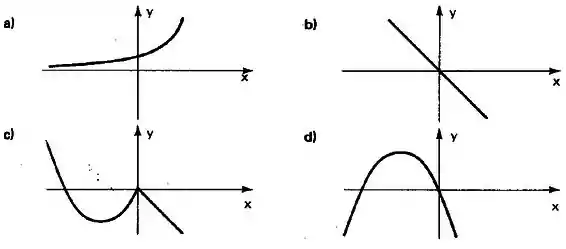
Para as funções em representadas abaixo qual é injetora? E sobrejetora? E bijetora?
Passo 1
a) A primeira função não é sobrejetora, pois ela não vai atingir todos os valores do contradomínio, nunca atingirá os elementos em y que são menores ou iguais a 0, ou seja a imagem não será igual ao CD.
No entanto, ela será injetora, pois todos os elementos do domínio (x) vão se relacionar a um elemento diferente do contradomínio (y).
Passo 2
b) Essa será bijetora, ou seja injetora e sobrejetora ao mesmo tempo. A imagem é igual ao CD e nunca dois elementos do domínio (x) vão se relacionar a um mesmo elemento do CD (y)
Passo 3
c) Será sobrejetora, pois atingirá todos os elementos possíveis do contradomínio. Mas não será injetora pois existem elementos do domínio que vão atingir o mesmo elemento no contradomínio. Observe só:
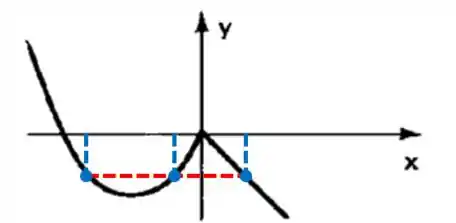
Viu?
Para 3 valores distintos de x, temos o mesmo valor de y associado. Toda vez que mais de um elemento x estiver associado a um mesmo y, você já pode concluir que essa função não é injetora.
Passo 4
Essa não será nem sobrejetora e nem injetora, observe bem:
- Ela não atingirá todos os elementos de y, pois tem um ponto de máximo. Ou seja, a imagem não será igual ao contradomínio.
- Ela tem valores de x que atingem o mesmo y.
Resposta
- Injetora
- Bijetora
- Sobrejetora
- Nem sobrejetora e nem injetora
Exercício Resolvido #2
Matemática Elementar – Gelson Iezzi e Carlos Murakami – 3ª edição – Pág. 192
Determine o valor de em de modo que a função de em definida por seja SOBREJETORA.
Passo 1
Para que a função seja sobrejetora, precisamos que a imagem seja igual ao contradomínio. Lembrando que o contradomínio é o conjunto que contém todas as imagens possíveis para a função.
Então o que a questão pede é achar quis valores de que satisfaçam isso. A gente vai fazer isso olhando o gráfico.
Passo 2
Vamos observar o gráfico da nossa função.
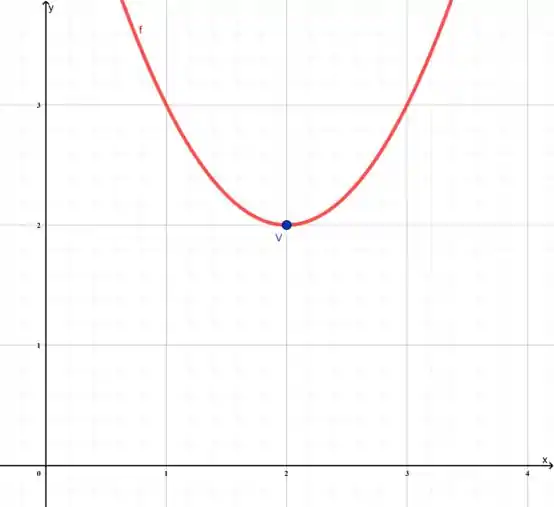
Perceba que o nosso vértice está no ponto , ou seja o nosso domínio(x) só atingirá valores maiores do que 2 no contradomínio. Vê se assim fica mais claro:
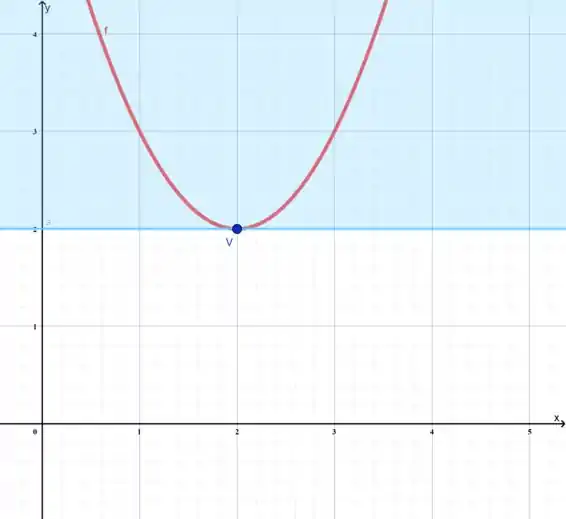
Isso significa que para a Imagem ser igual ao contra domínio, o nosso b precisa ser maior ou igual a 2.
Resposta
Exercício Resolvido #3
Elaboração Própria
Determine a inversa das funções abaixo:
Passo 1
- A função tem tanto o contradomínio quanto a imagem igual ao conjunto dos números reais e não existe mais de um para cada , dessa forma, ela é bijetora e invertível.
- Sabemos que essa função aí é uma parábola. Logo sabemos que a função não é bijetora, pois dois valores diferentes de podem resultar em um único valor de . Dessa maneira, não há inversa.
- Primeiramente, observamos que a função tem uma restrição no domínio: .
Isolando :
Trocando as variáveis, chegamos a inversa:
Passo 2
Passo 3
Apesar disso, vamos tentar inverter a função mesmo assim.
Isolando :
Trocando as variáveis, chegamos a inversa:
Verificamos que foi possível encontrar uma única expressão para a função inversa de . Dessa maneira, podemos concluir que tratava-se de uma função bijetora.
Resposta
- Não há
Exercício Resolvido #4
Elaboração Própria
Determine o valor de , sendo
Passo 1
A função tem tanto o contradomínio quanto a imagem igual ao conjunto dos números reais e não existe mais de um para cada , dessa forma, ela é bijetora e invertível. Isolando :
Trocando as variáveis, chegamos na inversa:
Passo 2
Agora é substituir valores como qualquer função e calcular a soma que o enunciado pediu:
Resposta
Exercício Resolvido #5
Elaboração Própria
Determine o valor de para que possua como inversa a função:
Passo 1
Essa pode parecer difícil, mas não é. Vamos pegar e tentar inverter normalmente:
Colocando o em evidência:
Substituindo variável por outra, chegamos a inversa:
Passo 2
Comparando com:
Concluímos que .