Funções Pares e Ímpares

Teoria

Sim, funções também podem ser classificadas como sendo pares ou impares e há ainda aquelas que não se prendem a rótulos e não são nenhuma das duas.

Mas essa classificação é um pouco diferente pra funções e a melhor forma de entender a paridade das funções é pensando em simetria.

Isso porque dizemos que uma função é par se ela é simétrica em relação ao eixo , que é o eixo vertical, como podemos ver na figura abaixo:

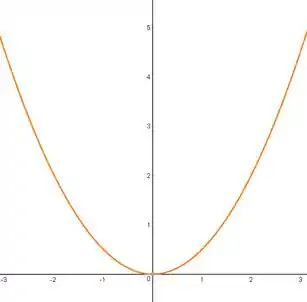
Repare que a função à esquerda do eixo vertical é igual à função à direita do eixo vertical, como se tivéssemos o reflexo num espelho. Escrevendo algebricamente, temos:

Ou seja, tanto faz se a o argumento é positivo ou negativo, o resultado da função é o mesmo!

São exemplos de funções pares:

Para o primeiro caso, além do gráfico, conseguimos também demonstrar algebricamente substituindo o por e tentando chegar à mesma expressão:

As funções ímpares, por sua vez, são simétricas em relação a origem , como a função cúbica abaixo:

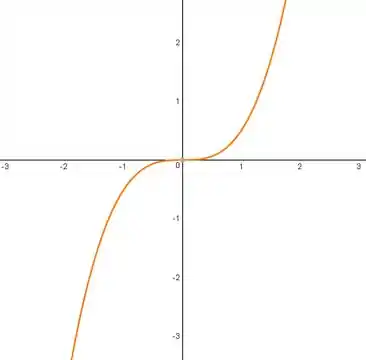
É como se pegássemos a parte da função à direita do eixo y e refletíssemos duas vezes, uma vez pra esquerda e outra pra baixo.

No fim, se pegarmos dois pontos opostos de mesmo módulo, por exemplo e , temos valores também opostos e que ficam a uma mesma distância da origem.

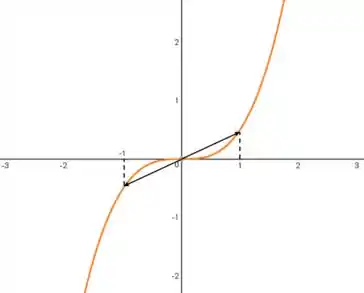
Podemos escrever isso algebricamente como:

Ou seja, quando o valor do argumento tiver o sinal oposto, o resultado da função também tem o sinal oposto!

São bons exemplos de funções impares:

Para o primeiro caso, veja que:

Por fim, temos aquelas funções que não se prendem aos rótulos e, portanto, não apresentam nenhuma das duas simetrias. Como:

Onde:

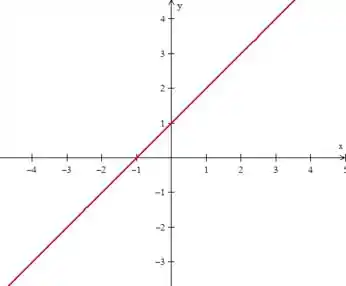
Que não tem simetria nem com o eixo , nem com a origem. E tá tudo bem!

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Verifique a paridade da função :

Calcule :

Verifique a paridade da função .

Passo 1

a) Bom, o primeiro passo é analisar . Para isso, calculamos :

Passo 2

Não é muito trivial verificar as condições de paridade agora – isto é, comparar com . Se preferir, podemos abrir as expressões:

E a verdade é que e . Ou seja, a função não é par nem ímpar!

Passo 3

b) Agora vamos obter usando as expressões abertas do passo 2:

Passo 4

c) Agora observamos que

E, portanto, a função é par!

Resposta

não tem paridade.
é par.

Exercício Resolvido #2

Elaboração Própria

Toda função quadrática é par?

Passo 1

Para mostrarmos que é falso, basta encontrarmos um contra exemplo.

Observe a função quadrática abaixo, dada por

Observe que essa função com certeza não é simétrica em relação ao eixo y.

Mostrando isso algebricamente, temos:

Na real, a nossa função quadrática só será uma função par quando o seu vértice estiver sobre o eixo y. Caso contrário, não.

Portanto, essa afirmativa é FALSA.

Resposta

Falso.

Exercício Resolvido #3

Elaboração Própria

Classifique as funções abaixo em pares, ímpares ou sem paridade.

b) c)

Passo 1

O primeiro com certeza não é nem par e nem ímpar, pois não há simetria nem em relação a y e nem em relação a origem.

SEM PARIDADE

Vamos ao segundo gráfico, observe que ele é simétrico em relação ao eixo y, portanto ele é par.

Por último, o terceiro: Ele será uma função ímpar pois esse gráfico é simétrico em relação a origem.

ÍMPAR

Agora um obs muito importante: Sempre que possível verifique se sua função é par ou ímpar algebricamente, pois gráficos podem nos enganar, pode parecer que é simétrico quando na verdade não é, beleza?

Resposta

SEM PARIDADE
PAR
ÍMPAR

Exercício Resolvido #4

Elaboração Própria

Verifique se a função é par.

Passo 1

Esse é um clássico exemplo que precisamos tomar cuidado

Sabe por que, se construirmos o gráfico dessa função. Veremos que ele vai aparecer da seguinte forma:

Daí você olha e diz: é claro que essa função é simétrica!

Vai com calmaaaaa!

Confere isso algebricamente, antes de afirmar qualquer coisa.

Ou seja,

Portanto, essa função NÃO é par.

Resposta

Não é par.

Exercício Resolvido #5

Elaboração Própria

Considere a afirmação a seguir:

A função possui um gráfico simétrico ao eixo y. A afirmação está:

a) Correta, pois a função é par

b) Correta, pois a função é ímpar

c) Falsa, pois a função é ímpar

d) Falsa, pois a função não possui paridade

e) Não tem como saber

Passo 1

Beleza, NÃO VAMOS FAZER O GRÁFICO DESSA FUNÇÃO, por motivos de: Preguiça kkkkkkkk

Mentira, é bem bizarro pensarmos num gráfico de uma função de 4º grau, você vai perder muito tempo de forma desnecessária. Em casos assim é bem melhor utilizarmos os métodos algébricos para descobrirmos o que a gente quer.

Primeiro, vamos verificar se a nossa função é par

Para isso, teremos: