Inequações produto-quociente
Produzido por Erick PinhoTeoria
Quando falamos sobre as inequações polinomiais, vimos que a gente tinha um passo a passo bem definido do que fazer:
- Isole todos os termos da inequação em um único lado;
- Ache as raízes da equação correspondente
- Esboce o gráfico e veja quais regiões satisfazem a condição da inequação ou teste valores nos intervalos formados pelas raízes.
Show, vimos o que fazer com inequações polinomiais, principalmente as do 1º e 2º grau, mas e se estivermos fazendo o produto ou o quociente de mais de uma equação?
É isso que vamos ver agora, simbora?
Inequações produto
Esse tipo de inequação ocorre quando temos um produto entre funções que sabemos fazer a análise de sinais.
Digamos que a inequação seja:
Temos uma inequação que é um produto de duas funções de grau.
O primeiro binômio é o e o segundo é .
Utilizando o que nós acabamos de aprender, podemos construir uma tabela de sinais para cada uma dessas funções, fazendo a respectiva análise do sinal de cada uma delas.
Vamos olhar a primeira função , sua raiz será:
Como o é negativo, a função é decrescente e será positiva, antes da raiz e negativa, depois. Temos então o seguinte gráfico:
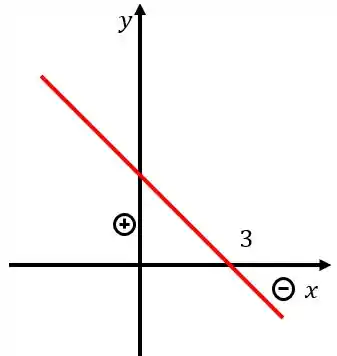
Já para a segunda parte, teremos como raiz:
Como aqui o é positivo, a função é crescente e tem valores negativos antes da raiz, e positivos depois! Ficamos então com o seguinte gráfico:
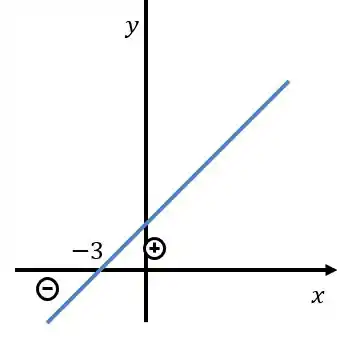
Agora, temos que juntar as duas partes, para isso vamos fazer o quadro de sinais:

Vamos entender como construímos esse quadro! Olhando para a primeira coluna, temos na primeira linha, a função que vamos analisar o sinal e nas linhas seguintes, as expressões que compõem essa função.
Nas demais células vamos colocar o sinal de cada função nos intervalos correspondentes. As células a esquerda de , indicam valores de menores que este número. As células entre e indicam valores nesse intervalo e as células a direita de indicam valores maiores que .
Foram escolhidos e não por acaso. Sempre escolhemos as raízes da função que estamos querendo analisar.
Vamos colocar os sinais da primeira função, que é positiva quando é menor que e depois é negativa:
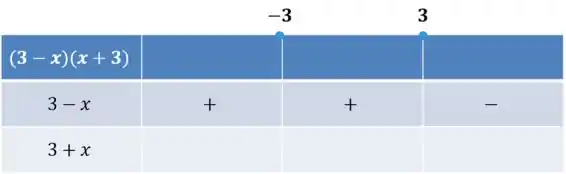
Agora, para a segunda parte, temos valores negativos antes de e positivos depois:
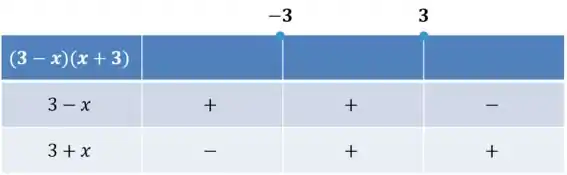
Como nossa inequação é a multiplicação das duas partes que analisamos, para achar o sinal da inequação nos intervalos, vamos multiplicar os sinais de cada uma dessas partes!
Lembrando que é importantíssimo respeitar as regrinhas dos sinais para produto e quociente:
- Sinais iguais
- Sinais diferentes
Temos então, sinal positivo para a inequação no intervalo do meio, onde os sinais são iguais, e para e , temos o sinal negativo, já que os sinais de cada parte são diferentes:
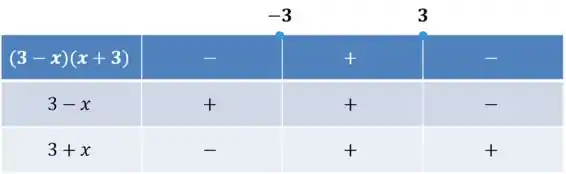
E é isso aí! Como queríamos resolver a inequação:
Olhando a tabela, temos que a solução será a parte positiva:
Além disso, como queremos saber os valores maiores ou iguais a zero na inequação, colocamos o intervalo com (menor ou igual) para incluir as raízes, que são os valores onde a inequação será igual a zero!
Show? É basicamente isso.
Inequações quociente
Quando você tiver inequações com quocientes, usamos a mesma lógica da seção anterior, a mesma tabela, o mesmo esquema igualzinho!
Por exemplo, para a inequação abaixo:
A solução é quase a mesma que nós acabamos de encontrar para , já que as duas inequações são formadas pelas mesmas partes.
A única diferença é que você tem que tirar o que faz o denominador dar 0! No caso, .
Seguimos a mesma lógica no nosso quadro de sinais, lembrando que nossas regrinhas de sinais valem tanto pro produto, quanto pro quociente!
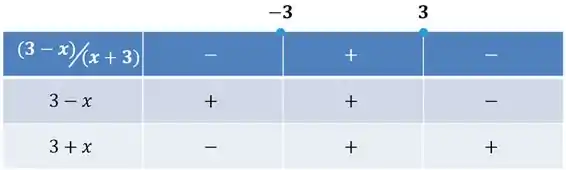
Por isso, chegamos no mesmo intervalo, só precisamos então excluir o da resposta, pra isso mudamos de (menor ou igual) para (menor apenas):
Prontinho! Com isso, conseguimos resolver inequações produto e quociente!
Inequações quociente
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine o conjunto solução que satisfaz a desigualdade .
Passo 1
Primeiro vamos arrumar a desigualdade, para ficar com a cara que você viu na teoria.
Passo 2
Agora surge a diferença de quadrados, que você conhece muito bem. Basta resolver-la para encontrar os monômios, ou seja, um polinômio de grau 1, que é uma função do 1º grau.
Passo 3
Vamos usar o macete da tabela para analisar os sinais:

Agora temos o intervalo em que a desigualdade é positiva e o intervalo em que ela será negativa. Como queremos positiva, temos:
Resposta
Exercício Resolvido #2
UFF, Cálculo IA-Lista 1, GMA, 2008-1, 8
Resolva a inequação:
Passo 1
Beleza, primeiramente vamos distribuir o termo elevado ao quadrado:
Substituindo, temos:
Jogando tudo para o mesmo lado sem pudor algum:
Opa, temos uma inequação de segundo grau limpinha agora!
Passo 2
Vamos achar as raízes, para então fazer o estudo do sinal:
Logo:
Passo 3
A partir disso, dividimos o domínio em intervalos limitados pelas raízes e testamos o sinal, que só muda quando passa na raiz, ou seja, podemos escolher qualquer valor nos intervalos gerados que garantiremos que o sinal não muda naquele intervalo. Eles serão:
Para o primeiro intervalo, podemos escolher :
Logo, ela é positiva nesse intervalo.
Para o segundo, podemos escolher o :
Logo, ela é negativa nesse intervalo.
Para o terceiro, podemos escolher :
Logo, ela é positiva nesse intervalo.
Passo 4
Voltando a inequação do problema, temos:
Queremos, portanto, o intervalo com valor negativo da expressão, ou seja:
A solução será, portanto:
Resposta
Exercício Resolvido #3
UFF, Cálculo IA-Lista 1, GMA, 2008-1, 9
Resolva a inequação:
Passo 1
Vamos primeiro juntar tudo num mesmo lado:
Agora, vamos deixar tudo no mesmo denominador:
Passo 2
Como o numerador está ao quadrado, o seu sinal vai ser sempre positivo, dessa forma, o sinal da expressão vai depender do denominador, que é positivo para e negativo do contrário.
Com isso, como queremos:
A solução será:
, pois nesse ponto o numerador zera e a expressão também, o que não satisfaz a desigualdade proposta, que cobra um valor maior que zero.
Resposta
Exercício Resolvido #4
Elaboração Própria
Qual a solução da inequação abaixo?
Passo 1
Vamo que vamo!
Para início de conversa, vamos estudar o sinal da função:
Depois, iremos ver para que intervalo do domínio,
Só que, antes, teremos que definir o domínio de .
Passo 2
A única restrição ao domínio de é o denominador, já que a função não apresenta raízes, nem logaritmos, nem nada. Vamos olhar para o denominador:
Passo 3
Hora de analisar o sinal da função. Repare que a função já está toda fatorada em monômios do primeiro grau: .
Vamos analisar o sinal desses monômios separadamente e depois usar a tabelinha. Para analisar, basta achar as raízes e ver se a função é crescente ou decrescente.
Analisando :
A função é decrescente, então, é positiva antes de e negativa depois de .
Analisando :
A função é crescente, então, é negativa antes de e positiva depois de .
Analisando :
A função é crescente, então, é negativa antes de e positiva depois de .
Passo 4
Hora de usar a tabelinha!
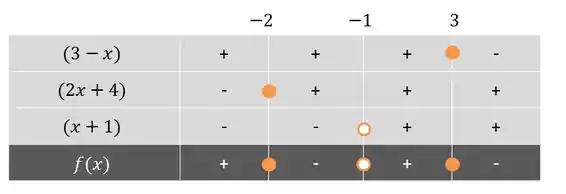
Repare que representei com bolinhas fechadas as raízes (zeros da função) que pertencem ao domínio e com bolinhas abertas, as raízes que não pertencem ao domínio.
Resposta
Como queremos , o intervalo solução é:
Exercício Resolvido #5
Elaboração Própria
Resolva:
Passo 1
Temos aí dois produtos que mudam de sinal. Vamos pegar as raízes deles, marcar e tabela e estudar o sinal.
Passo 2
A partir desses valores, montamos uma tabela marota:

Agora colocamos o sinal em cada intervalo:

E fazemos o estudo do sinal para determinar quão sinal da expressão de interesse:

Passo 3
Como queremos que:
Então podemos pensar que a solução será a união dos intervalos positivos da tabela:
Só que tem um detalhe bem importante! Lembra que lá atrás vimos 3 valores que anulam o produto ? Esses valores eram:
Repara que a solução que achamos, ou , inclui . Sendo que, como acabamos de ver, esse não pode ser solução da inequação, pois
Portanto, a solução da inequação é:
Ou, se você preferir:
Resposta
Exercício Resolvido #6
Elaboração Própria
Resolva:
Passo 1
Vamos lá. Lembre-se primeiro que não podemos usar produto cruzado aqui, portanto, vamos jogar tudo no mesmo lado:
Juntando tudo no mesmo denominador:
Passo 2
Agora, pegamos as expressões relevantes, marcamos seus zeros e fazemos uma tabela de sinais:
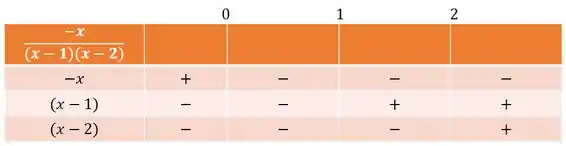
Agora, fazendo estudo do sinais, vemos o sinal da expressão:
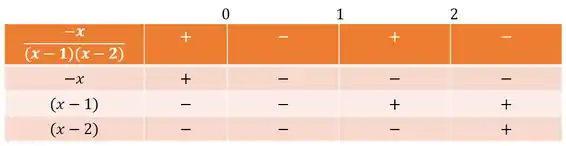
Como queremos:
Pegamos os valores negativos e, portanto, a solução é:
Resposta
Exercício Resolvido #7
Elaboração Própria
Resolva a inequação a seguir e apresente o quadro de sinais e os possíveis valores de x.
Passo 1
Vamos lá!! Temos nessa questão uma inequação envolvendo um produto:
Onde e
Vamos encontrar as raízes deles e montar a tabelinha marota!

Passo 2
Analisando , temos
Visualmente teremos

Analisando , temos
O esboço seria
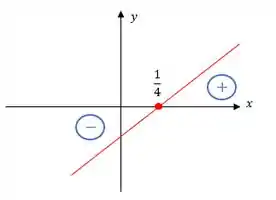
Beleza?!
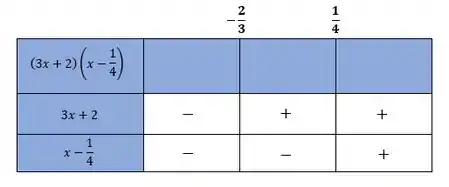
Passo 3
A partir desses valores, vamos montar a tabelinha para estudar os sinais:
Agora fazendo o estudo dos sinais, teremos
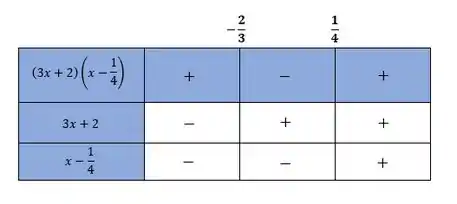
Como queremos
Vamos selecionar os intervalos aonde o sinal é positivo! Assim, nosso conjunto solução é
Resposta
Exercício Resolvido #8
Elaboração Própria
O conjunto solução da inequação abaixo é
Passo 1
Vamos lá!! Temos nessa questão uma inequação envolvendo um produto e um quociente:
Onde
E
Vamos encontrar as raízes de cada uma dessas funções e montar a tabelinha marota para estudar os sinais?!

Passo 2
Vamos encontrar as raízes de cada uma das funções!
Analisando , temos
Passando o 4 para o lado direito da igualdade
Dividindo ambos os lados da igualdade por
Visualmente teremos
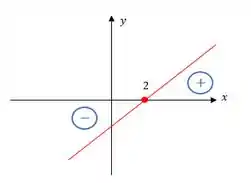
Agora vamos encontrar a raíz de
Passando o 2 para o outro lado, temos
O esboço seria
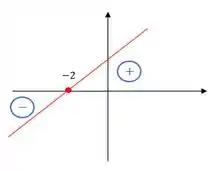
E por fim, vamos encontrar a raíz da
Passando o para o lado direito da igualdade, temos
Dividindo tudo por 4
Visualmente, teríamos
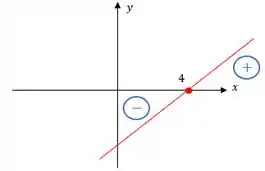
Beleza?!
Passo 3
A partir desses valores, vamos montar a tabelinha para estudar os sinais:
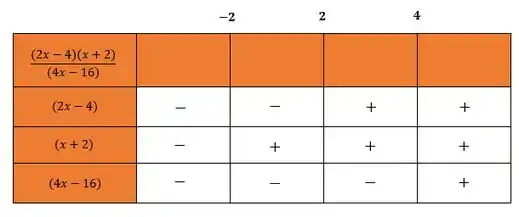
Agora fazendo o estudo dos sinais, teremos
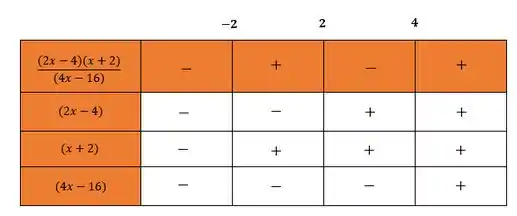
Como queremos
Vamos selecionar os intervalos aonde o sinal é positivo! Assim, nosso conjunto solução é
Resposta
Exercício Resolvido #9
Elaboração Própria
Resolva a inequação a seguir e apresente o quadro de sinais e os possíveis valores de x.
Passo 1
Vamos lá!! Temos nessa questão uma inequação envolvendo um produto entre termos:
Onde
Vamos encontrar as raízes de cada uma dessas funções e montar a tabelinha marota para estudar os sinais?!

Passo 2
Vamos encontrar as raízes de cada uma das funções!
Para encontrarmos as raízes da equação
Utilizaremos a fórmula de Bhaskara
Beleza?!

Primeira coisa que precisamos fazer é identificar quem é o , e . Lembra da carinha da nossa equação do 2º grau? Ela tem essa carinha aqui
Então, comparando com a nossa equação
Conseguimos encontrar os valores de , e :
Beleza?! Agora vamos utilizar esses valores para encontrar o :
Substituindo os valores , e , temos
Fazendo as continhas, temos
Agora podemos substituir o valor de e os demais valores na fórmula de Bhaskara:
Teremos então duas raízes:
E
Portanto, as raízes da equação são e !
Visualmente, teríamos
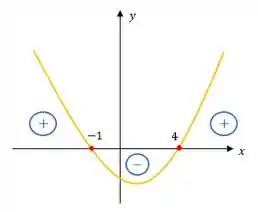
Beleeeza?!
Passo 3
Agora precisamos encontrar a raíz da função
Para isso, iremos igualar a função a
E passar o para o outro lado
O esboço seria
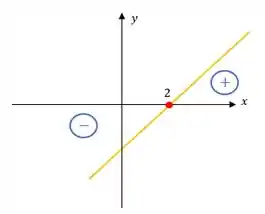
Passo 4
A partir desses valores, vamos montar a tabelinha para estudar os sinais:
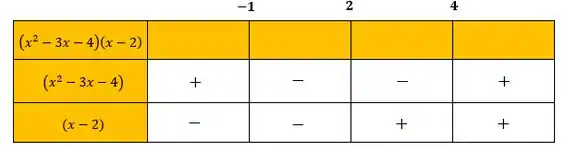
Agora fazendo o estudo dos sinais, teremos
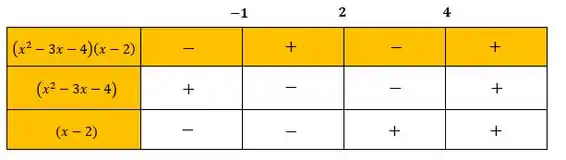
Como queremos
Vamos selecionar os intervalos aonde o sinal é positivo! Assim, nosso conjunto solução é
Resposta
Exercício Resolvido #10
Elaboração Própria
A solução da inequação abaixo é:
Passo 1
Vamos lá!! Temos nessa questão uma inequação envolvendo um produto:
Onde e
Vamos encontrar as raízes deles e montar a tabelinha marota!

Passo 2
Analisando , temos
Visualmente teremos
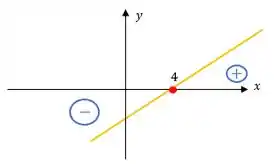
Analisando , temos
O esboço seria
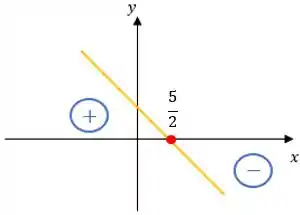
Beleza?!
Passo 3
A partir desses valores, vamos montar a tabelinha para estudar os sinais:
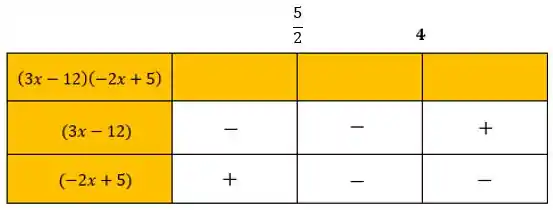
Agora fazendo o estudo dos sinais, teremos
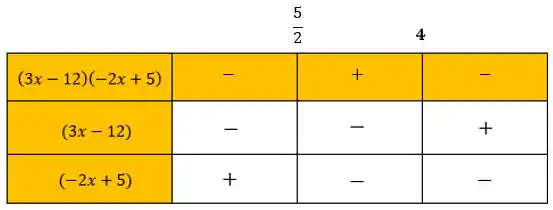
Como queremos
Vamos selecionar os intervalos aonde o sinal é positivo! Assim, nosso conjunto solução é
Resposta
Letra A