Inequação Modular
Produzido por Erick PinhoTeoria
Fala aí! Hoje vamos aprender sobre inequações modulares e como resolver exercícios envolvendo esses caras.
Tá preparado? Então vem comigo 😆
⭐ Veja também ⭐
- Exercícios resolvidos de inequações modulares.
- Inequações polinomiais.
- Inequações exponenciais e logarítmicas.
- Inequações trigonométricas.
O que é uma Inequação Modular?
As inequações modulares que a gente vai ver são expressões que envolvem sinais de desigualdade e incógnitas dentro de módulos. Mais ou menos assim ó:
Pra entender o que vamos discutir aqui, é extremamente importante que você esteja dominando aquela definição clássica do módulo de um número!
Se tiver se esquecido, vale refrescar a memória:
Belezinha? Com base nisso aí, saca esse exemplo:
Com essa definição, a gente consegue formalizar aquela noção de que “módulo é só desconsiderar o sinal”.
Tranquilo?
Vamos pensar no módulo como distância pra facilitar as coisas. Da seguinte forma:
O
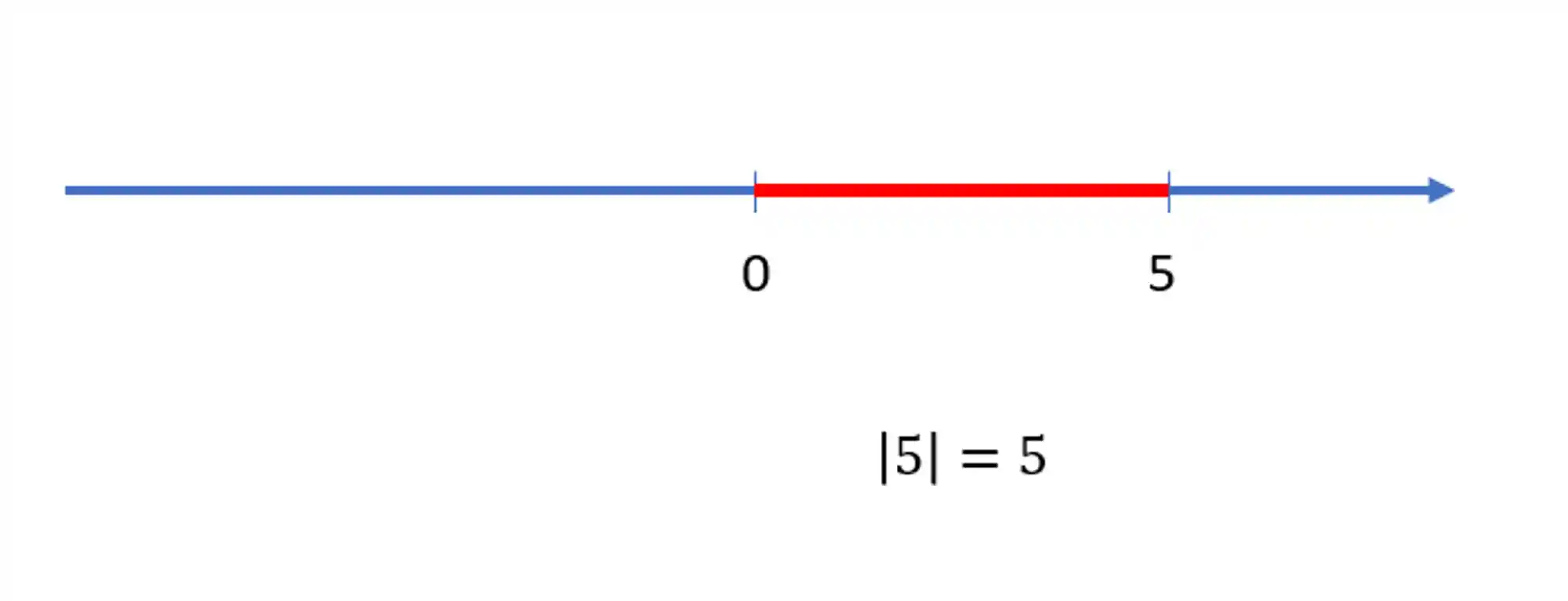
Só que existe um outro número na reta real que tem exatamente essa mesma distância até o 0. Consegue adivinhar qual é?
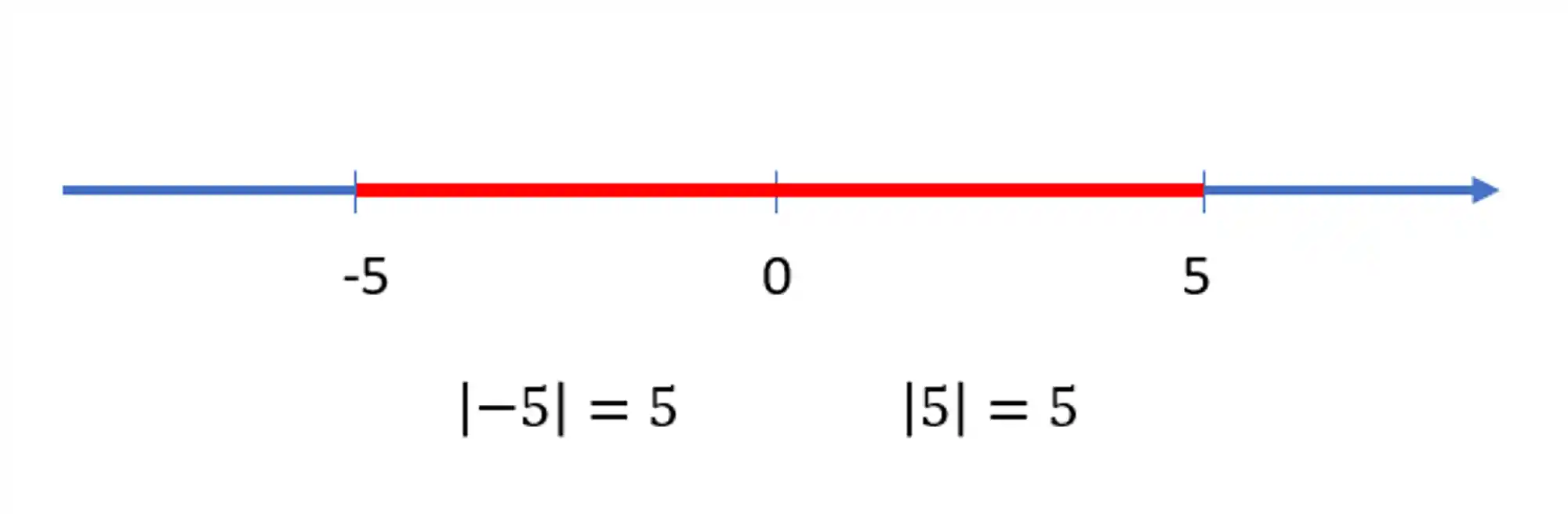
Isso mesmo! É o
Agora vamos um pouquinho além 😉
Se eu te falar que o módulo de
Só que, de novo, existe um número lá do lado dos negativos que vai ter a mesma distância que
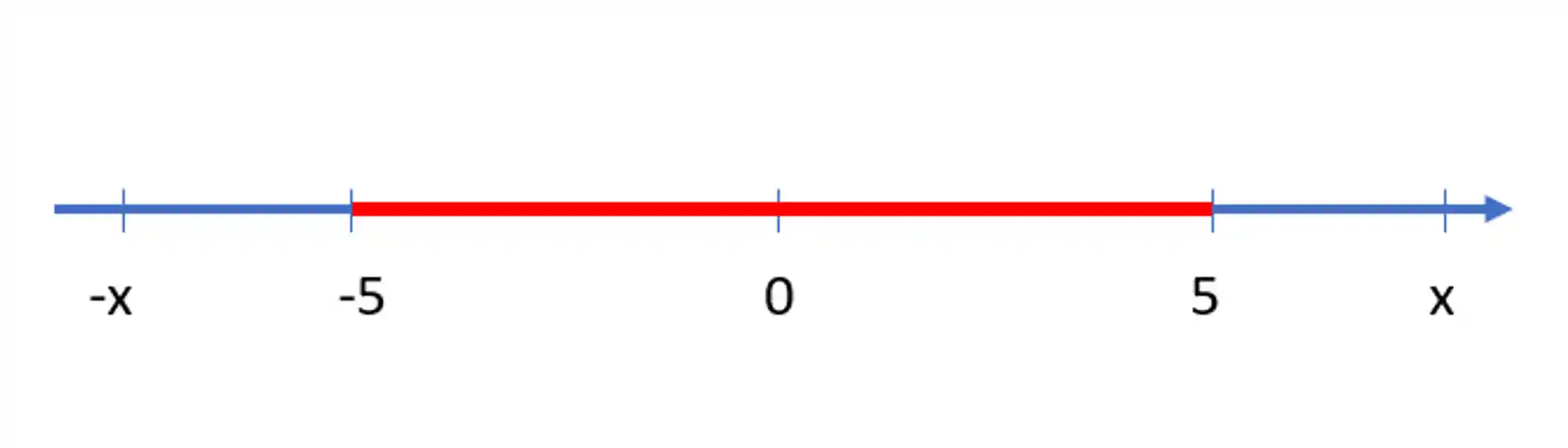
Observando essa reta aí, a gente pode concluir duas coisas:
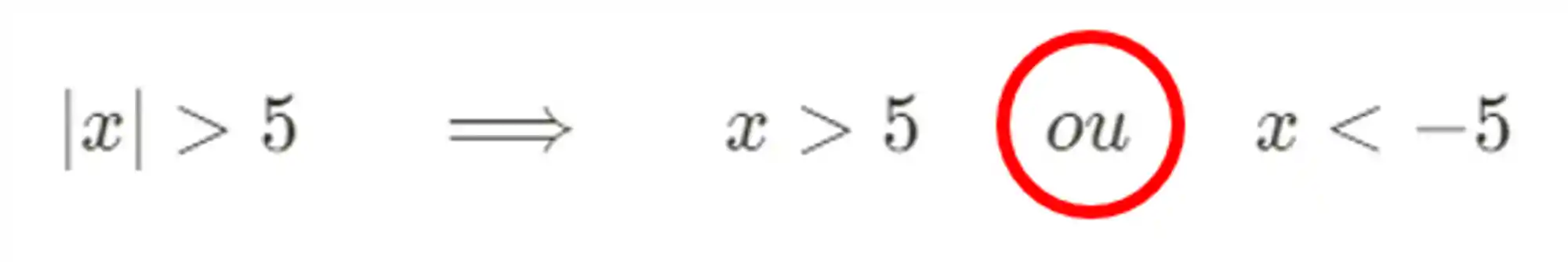
Agora, vamos pensar nesse caso aqui:
Dessa vez, a distância entre

Então a gente pode dizer isso aqui:
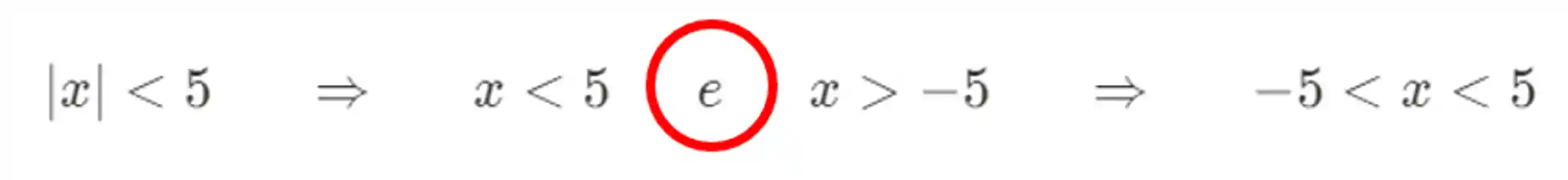
Maravilha! Se você entendeu isso aí, já estamos com 80% do caminho andado 😆
Repara que antes eu circulei um “ou”, ali em cima. Mas dessa vez apareceu um “e”. Isso não é arbitrário não viu? Já te explico na próxima parte.
Antes de prosseguirmos, se você ainda ficou com dúvida, confere esse vídeozinho aqui com uma explicação bem detalhada 👇
Agora, vamos ver como resolver uma inequação modular de fato.
Como resolver uma inequação modular
A gente vai dividir as resoluções em dois casos: módulo menor que um número e módulo maior que um número. Tal como mostrei aí em cima.
Caso 1: Módulo menor que um número
Esse caso tem essa carinha aqui:
Da mesma forma que fizemos anteriormente, a distância de todo aquele termo ali do lado direito até o zero vai ser menor que 4. Então, a gente procede assim:
E aí resolvemos uma inequação de cada vez. Se liga:
Agora a outra:
Beleza! Agora é só juntar as duas respostas!
Caso 2: Módulo maior que um número
Dessa vez, a gente tem algo desse tipo aqui:
Então, a gente vai ter duas expressões, tal como fizemos lá no começo:
Olha aquele ou aí de novo! Ele tá aí pra mostrar que a nossa solução nesse caso aqui vai ser a união de dois intervalos, e não mais a interseção 😁
Em sequência, vamos resolver a primeira inequação:
E a segunda:
Logo, a solução é:
Belezinha?
Então bora complicar um pouquinho mais com nossos exercícios resolvidos passo a passo ☺️