Teoria
Os intervalos numéricos são subconjuntos dos números reais, representados em uma reta. Bora entender como eles funcionam?!
Tipos de Intervalos Reais
Hoje vamos aprender como representar os conjuntos numéricos utilizando uma reta!

Lembrando que o conjunto numérico dos números reais, inclui os números naturais, inteiros e racionais. Você pode clicar aqui pra relembrar o que são esses conjuntos numéricos!
Intervalo Fechado
Olha esse subconjunto aqui:
Esse é um intervalo fechado! Sempre que tivermos um sinal de menor ou igual, ou maior ou igual, estamos incluindo os números das extremidades, então o intervalo é fechado!
A representação na reta é feita com uma bolinha fechada, assim:

No vídeo abaixo, a gente fala um pouquinho mais sobre intervalos fechados, abertos e mistos, além das operações entre os intervalos! Dá só uma conferida! 😉 👇
Intervalo Aberto
Agora vamos ver um exemplo de intervalo aberto:
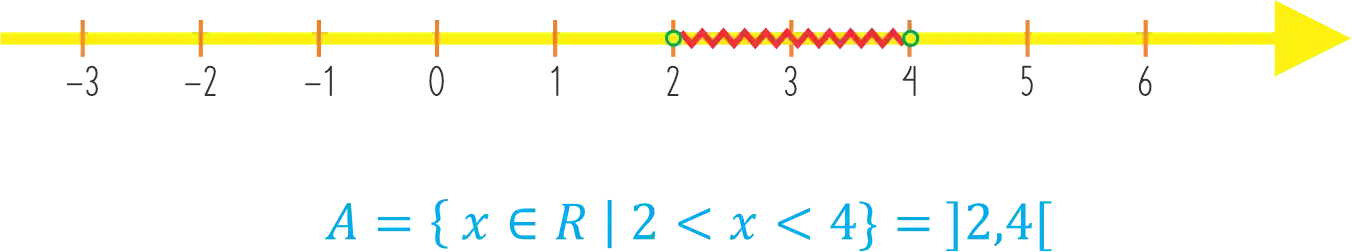
Aqui a gente não tem mistério! Temos um intervalo aberto quando o conjunto é delimitado por sinais de maior ou menor, ele exclui os números das extremidades. e é representado na reta por uma bolinha aberta.
Intervalo Aberto à Direita
O intervalo aberto à direita tem um sinal de menor ou igual, incluindo o menor valor do intervalo, e um sinal de menor, excluindo o maior valor. Por exemplo:
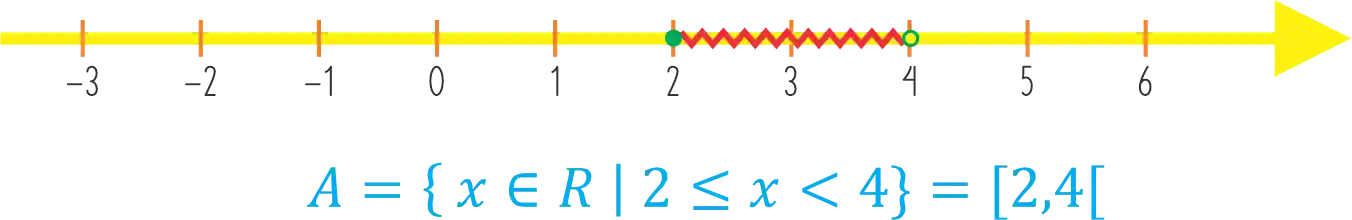
Já o intervalo aberto à esquerda inclui o maior valor e exclui o menor. Assim:
Podemos representar na reta:

União e Intersecção de Intervalos
Como os intervalos são subconjuntos dos números reais, a gente pode fazer algumas operações com eles, como união e intersecção!
Saca só esse intervalo:
Toda vez que temos o termo “ou” estamos falando de uma união. Podemos representar essa união da seguinte forma na reta:

Podemos escrever esse intervalo da seguinte forma:
Agora, e se quiséssemos a intersecção dos intervalos acima? Teríamos um conjunto vazio, já que não existe nenhum número em comum entre os dois subconjuntos!
Agora vamos praticar com exercícios?!
União e Intersecção de Intervalos
Exercícios Resolvidos
Exercício Resolvido #1
Reescrever os conjuntos abaixo usando a notação de intervalo e, a seguir, representá-los graficamente.
Passo 1
Bom, é aquilo que sempre digo, é do começo que se começa (tá, isso tinha ficado melhor na minha cabeça)
Veja que temos que é estritamente maior que e ele não tem um máximo, pode ir embora até quando quiser. Ele tem apenas um chão, um valor do qual ele não passa, e nesse caso, ele nunca chega àquele valor , por conta da desigualdade. Vamos ter o seguinte:
A representação gráfica será (em vermelho):
![]()
Como temos um intervalo aberto em , precisamos de uma bolinha aberta nele.
Passo 2
Show, bora pro próximo!
Aqui temos que está dentro de um intervalo que tem o como maior valor e como seu menor valor, e pode assumir quaisquer um dos dois valores inclusive. Sendo assim, temos um intervalo fechado:
A representação gráfica será (em vermelho):
![]()
Como temos um intervalo fechado em e em , a bolinha precisa ser fechada nesses pontos.
Passo 3
Dá uma olhada nessa aqui agora:
MUITA ATENÇÃO NESSE DETALHE: temos um OU ali, então teremos uma UNIÃO de intervalos!
Vamos olhar um de cada vez. O primeiro diz que pode ser qualquer valor menor que e pode ser inclusive. Então o intervalo é fechado em e aberto no infinito negativo:
E o segundo é um intervalo aberto em e fechado em , isso porque temos apenas o sinal de desigual em mas temos um sinal de igualdade ali também em .
Ora, agora vamos uni-los:
A representação gráfica é a seguinte (lembrando que bola fechada é no intervalo fechado e bola aberta é no intervalo aberto):
![]()
Passo 4
Olha só essa última:
MUITA ATENÇÃO NESSE DETALHE: temos um OU ali, então teremos uma UNIÃO de intervalos!
Vamos olhar um de cada vez. O primeiro diz que pode ser qualquer valor menor que 0. Então o intervalo é aberto em 0 e aberto no infinito negativo:
E o segundo é um intervalo aberto em e em , isso porque temos apenas o sinal de desigual em e :
Por último, temos um intervalo que diz que é estritamente maior que , então teremos um intervalo aberto em :
Ora, agora vamos uni-los:
A representação gráfica é a seguinte (lembrando que bola fechada é no intervalo fechado e bola aberta é no intervalo aberto):
![]()
Resposta
![]()
![]()
![]()
![]()
Exercício Resolvido #2
Representar os conjuntos abaixo, dados graficamente pela parte pintada em vermelho, usando a notação de intervalo e a notação de desigualdades.


![]()
![]()
Passo 1
Antes de começar a resolver, vamos entender as notações e o que a figura quer dizer!
Repara na linha que temos umas bolinhas vazias e umas todas preenchidas da cor vermelho. Elas vão ser chamadas de bolas abertas e fechadas, respectivamente.
E o que cada uma representa?
- Bola abertaintervalo aberto, ou seja, aquele número não pertence ao intervalo. A gente representa com um parênteses ou com um colchete virado para fora. Você pode escolher parênteses ou colchetes, ok?
- Bola fechadaintervalo fechado, ou seja, aquele número pertence ao intervalo. A gente representa com um colchete virado para dentro.
Passo 2
Bora fazer essas coisas do começo:

Então as extremidades do intervalo são e , com as bolinhas abertas neles. Então temos:
Essa foi a notação de intervalo, vamos fazer a de desigualdades. Perceba que estamos falando da reta real e temos que (um número real qualquer) está entre e , então:
Foi um bom começo né? Vamos continuar arrasando.
Passo 3

Aqui temos a união de intervalos, percebe?
Vamos escrever em intervalo o primeiro tracinho vermelho, que tem uma bola aberta em :
A gente a setinha ta indo em direção a um número negativo muito grande, a gente usa essa representação com , ok?!
No segundo tracinho vermelho temos um intervalo aberto tanto em quanto em :
O terceiro tracinho vermelho tem uma bolinha aberta em e segue para o infinito:
Então o intervalo é a união dos três que encontramos agora:
Vamos escrever agora em notação de desigualdades. Perceba que estamos falando da reta real e temos que (um número real qualquer) menor que OU ele está entre OU ele é maior que :
Cada símbolo de união corresponde à palavra OU na notação de desigualdades.
Passo 4
![]()
Agora temos um aí só pra te colocar medo! Hahahaha mas relaxa, o processo é o mesmo!
Temos ali uma bolinha fechada em e ponto, não tem tracinho nenhum. O que isso quer dizer? Quer dizer apenas que assume o valor , bem simples e objetivo.
Já o outro tracinho, nos mostra um intervalo que de vai de a , ambos com bolinha aberta. Vamos escrever o intervalo:
Lembrando que por mais que tenhamos apenas um número, só podemos unir CONJUNTOS, então escrevemos o número como um conjunto unitário (colocamos chaves nele)
Maneiro né? Bora escrever na notação de desigualdades. Perceba que estamos falando da reta real e temos que (um número real qualquer) é igual a OU ele está entre :
Cada símbolo de união corresponde à palavra OU na notação de desigualdades.
Passo 5
![]()
NOSSSSAAAAAA AGORA EU ENTREGO PRA DEUS!
Não faça isso, você verá que é a mesma coisa!!! Agora temos a união de quatro intervalinhos.
Olhando pro primeiro:
Agora olhando pro segundo:
Perceba que agora temos uma bolinha fechada em , então o intervalo foi fechadinho nele.
Olhando por terceiro:
Pois é, esse é somente um número porque temos só uma bolinha e pronto. Agora olhando pro quarto tracinho:
Show, bora unir essa galera:
Lembrando que por mais que tenhamos apenas um número, só podemos unir CONJUNTOS, então escrevemos o número como um conjunto unitário (colocamos chaves nele)
Agora passando isso para notação de desigualdades. Perceba que estamos falando da reta real e temos que (um número real qualquer) é menor que OU ele está entre OU ele é igual a OU ele é maior que :
Cada símbolo de união corresponde à palavra OU na notação de desigualdades.
Resposta
Exercício Resolvido #3
Dados os conjuntos e , efetue as operações pedidas e dê as respostas na notação de intervalo.
Passo 1
Primeiramente, vamos dar uma olhada em nossos dois intervalos, para ficar mais claro:
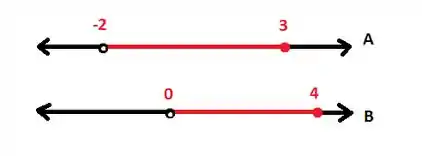
Vamos começar com a letra
Essa operação significa que vamos unir os dois intervalos, que graficamente seria o seguinte:
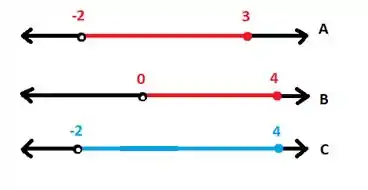
Perceba que a bolinha aberta some na união!!! Então o intervalo da união é:
Passo 2
A próxima letra pede:
Agora, não vamos unir os termos, vamos ver quais termos estão nos dois intervalos ao mesmo tempo! Olha o desenho:
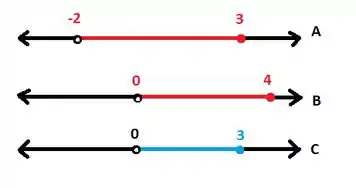
Agora é só escrever como intervalo:
Passo 3
Dá uma olhada nessa aqui:
Agora nós precisamos pegar o intervalo e tirar todos os elementos que estão em . Novamente, olhe o desenho (desenhos são as melhores técnicas para esse tipo de questão):
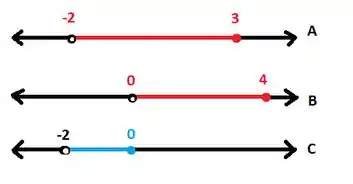
Agora é só escrever na notação de intervalo:
Passo 4
Olhaaaaaa, já estamos na última! Você tá indo bem, só mais uma, vem:
Então, a agora é justamente o contrário: vamos pegar o conjunto e tirar todos os elementos que estão no conjunto também. Olha o desenho de como fica:
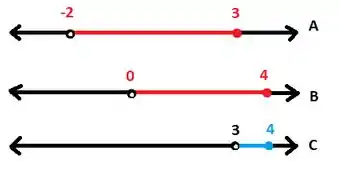
Perceba que temos uma bolinha aberta agora no , isso aconteceu porque estava no intervalo e no , portanto tivemos que tirá-lo dessa brincadeira! Agora escrevendo com a notação de intervalo:
FIMMM!
Resposta
Exercício Resolvido #4
Sejam os intervalos reais é correto afirmar que:
Passo 1
Ok, dá pra ver que tem muita conta pra fazer, mas vamos nos adiantar logo em algumas coisas.
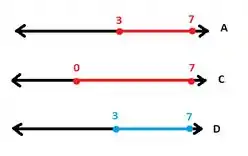
Guarda isso aí!
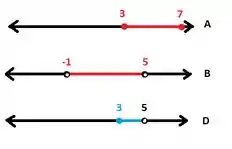
Falta só mais umazinha:
Passo 2
Agora que já fizemos nosso esboço, vamos atacar as alternativas!
Olha como fica o desenho:
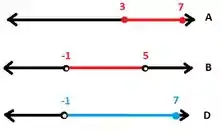
Lembrando que a primeira reta é e . Escrevendo em notação de intervalo:
Lembrando também que
Passo 3
Próxima alternativa:
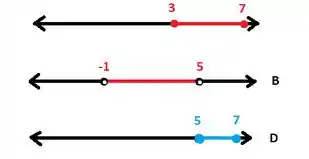
Olhe só o desenho de como o lado esquerdo fica:
Lembrando que a primeira reta representa e . Escrevendo em forma de intervalo:
Agora vamos ver o desenho de :
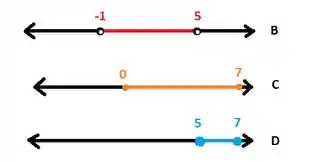
Perceba que são iguais, ou seja, essa está correta!!!
Passo 4
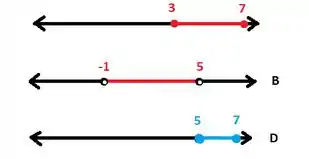
Olha só o desenho de como fica isso (lembrando que ):
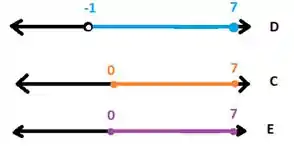
Passando isso pra notação de intervalo:
Logo, essa afirmação não é verdade.
Passo 5
Saca só como fica o desenho dessa parada (lembrando que ):
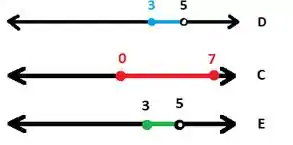
Escrevendo isso na notação de intervalo:
Portanto, esta não está certa.
Passo 6
Olha essa agora:
Se liga como fica o desenho (lembrando que ):
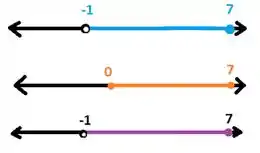
Passando isso pra notação de intervalo, ficamos com:
Lembrando que
Resposta
Letra
Exercício Resolvido #5
Dados os conjuntos
Escreva na notação de intervalo e represente graficamente o conjunto
Passo 1
Você que me acompanha aqui, sabe que agora eu diria pra começar do começo. Mas qual é o fuc***ng começo? Hahaha vamos começar dos parênteses ok?
Precisamos de , saca só o desenho:
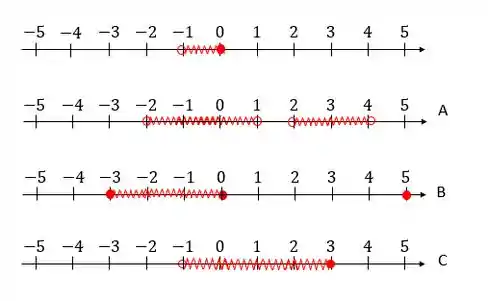
Essa primeira linha tem exatamente aquilo que procuramos: a interseção entre os três conjuntos, ou seja, aqueles números que estão presentes nos três conjuntos. Na notação de intervalo:
Passo 2
Agora vamos atrás do :
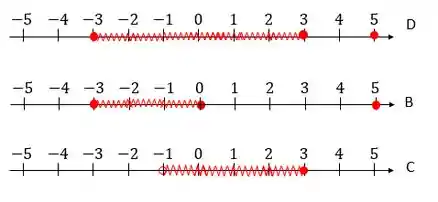
Veja que
Escrevendo na notação de intervalo:
Mas o que a questão quer é justamente o complementar disto, ou seja, tudo aquilo na reta que não seja o . Se liga como fica no desenho:
![]()
Percceba que as bolinhas fechadas viram bolinhas abertas e preenchemos tudo aquilo que estava preenchido. Escrevendo isso na notação de intervalo:
Passo 3
Maneiro, esse cara ta estranho, mas vida que segue! Vamos agora realizar a operação:
Escrevendo na notação de intervalo:
Perceba que são intervalos/conjuntos disjuntos, então não temos como simplificar esse termo. Pensa neles como quatro tracinhos numa reta que não se tocam.
Passo 4
Vamos enfim para o último passo, que é realizar a última operação:
Então, na representação gráfica, ficamos com:
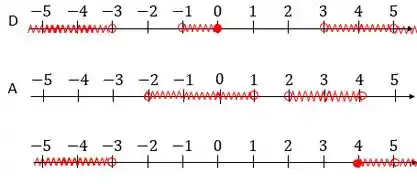
A última linha nos dá o resultado dessa contarada toda. Vamos escrever isso na notação de intervalo: