Equação de Laplace em regiões infinitas
Produzido por Carolina SabaTeoria
Introdução
Vimos as aplicações de EDP’s somente para regiões finitas, não é mesmo? Mas e para regiões infinitas será que é possível modelar com a utilização de EDP’s? Vamos ver que é possível e é bem semelhante ao já estudado anteriormente.
Vamos ver neste capítulo a Equação de Laplace para regiões infinitas! Calma, não se assustem. Você verá que a diferença estará basicamente nas condições de contorno.
Vimos anteriormente que a equação de Laplace para regiões bidimensionais é da seguinte forma:
Qual será a diferença então? Não teremos mais um retângulo, mas sim uma região semelhante a ele, porém infinita em uma das direções, ou seja, pode ser infinito na direção ou
Você deve estar se perguntando como resolver esse tipo de questão. Bom, diferentemente do caso de regiões finitas, poderá ser dada alguma informação das bordas quando ou tende a infinito (vai depender do tipo de questão). Assim, pode ser dado, por exemplo, um limite, ou seja, o valor para o qual tende quando ou tende a infinito.
Outra informação importante é que neste tipo de questão sempre estaremos trabalhando com a hipótese de funções limitadas no infinito, ou seja, o valor de ou deve ser limitado. Assim, mesmo que não seja dado o limite de no infinito, este valor é obrigatoriamente um número finito.
Para entender melhor, observe a figura a seguir:
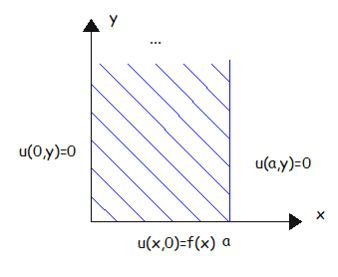
Veja que temos uma faixa semi-infinita na direção . Assim, na resolução de um algum problema que envolva essa região ele pode, por exemplo, dizer qual o valor que tende quando
Método de resolução
Agora vamos resolver esse exemplo:
Essas são as condições que o problema dá. Veja que foi dito que , ou seja ,foi dada informação de quando .
Passo 1: Separação de variáveis
Bom, vamos utilizar o mesmo método de sempre. Devemos encontrar uma solução do tipo . Como essa solução deve satisfazer a Equação de Laplace, temos:
Agora nós passamos tudo que tem para um lado e o que tem para o outro:
Assim, encontramos as seguintes equações características:
Aplicando a separação de variáveis para as condições do problema:
Sempre deixamos por último a condição que é uma função, nesse caso, .
Então, temos o seguinte:
Passo 2: Resolver o problema que tem duas condições (de contorno)
Como a função é a que possui duas condições de contorno, vamos resolver primeiro o problema em , temos então:
Já vimos este tipo de problema anteriormente e a solução vale:
Se você não lembra, não se preocupe, vou mostrar novamente o passo a passo para chegar nessa solução:
Esta equação tem solução apenas para . Assim podemos dizer que Portanto, a equação característica dessa EDO é a seguinte:
Assim, a equação geral vale:
Aplicando as condições de contorno:
Assim, a solução do problema é:
Como nesta questão , então:
Repare que, nos denominadores de e temos e não , pois a condição do problema é . Da mesma forma que, nos capítulos anteriores, era o comprimento da barra ou da corda em , aqui é o comprimento do lado do retângulo em .
Passo 3: Tendo os valores de , resolver a outra EDO
Beleza, agora temos que resolver o problema em , temos:
A equação característica dessa EDO é a seguinte:
Já vimos que , não é? Então, as soluções dessa EDO são do tipo:
Aplicando a condição temos que tomar cuidado, uma vez que quando o termo tende a infinito, o que não está de acordo com o queremos. Queremos que ! Assim, deverá ser igual a zero e, portanto a solução fundamental será da forma:
Então, podemos escrever o seguinte:
Passo 4: Escrever como série e achar os coeficientes da série
Como as combinações lineares de também são soluções do problema temos que:
Agora vamos usar a condição que faltou:.
Repare que o coeficiente dos termos dessa série é tudo o que está no colchete! Ou seja, que não depende de .Reescrevendo, temos que:
Se e são seccionalmente contínuas, então essa é uma Série de Fourier de senos. Fazendo uma extensão ímpar de , podemos dizer que:
Repare que o período da extensão é , não ! Por isso apareceram esses ’s na integral, tome cuidado. O veio do denominador do seno. Dessa forma, encontramos os coeficientes da série. Então, substituímos em:
Pronto, essa é a resposta. Bem parecido com o que temos visto, não é?
Análise Geral
Agora que já analisamos regiões infinitas no retângulo, vamos considerar o caso da equação de Laplace no disco para regiões infinitas. Novamente, será muito parecido com o que foi apresentado antes, o que vai mudar serão apenas as condições de contorno. Antes nós estávamos preocupados com a região interior ao disco, agora queremos a parte exterior a ele, ou seja, uma região ilimitada. Vamos relembrar a equação de Laplace para discos:
Vimos nos capítulos anteriores que a função de temperatura pode ser escrita da seguinte forma:
Onde , deve obrigatoriamente ser periódica de período . Assim, as únicas funções possíveis são as trigonométricas e a função constante. Qualquer outra função não é considerada válida na resolução do problema. Se você não se lembra disso, não se preocupe! Esta parte está bem explicada no capítulo anterior!
E a função ? Conforme apresentado no capítulo anterior ela apresenta algumas limitações, que variam de acordo com cada tipo de problema. No caso das regiões infinitas, estas limitações serão mais bem abordadas no método de resolução. Então não se preocupe no exercício resolvido você entenderá muito bem esse assunto.
Método de resolução
Vamos resolver esse exemplo:
Ou seja, estamos analisando uma região infinita de raio .
Devemos supor que está bem definida e é limitada para . (Esta hipótese será considerada em todos os exercícios deste conteúdo).
Essas são, portanto, as condições que o problema dá. Então, como resolver?
Passo 1: Separação de variáveis
Bom, vamos utilizar o mesmo método de sempre. Devemos encontrar uma solução do tipo . Como essa solução deve satisfazer a Equação de Laplace, temos que:
Colocando em evidência, temos que:
Assim, passando para a esquerda e para a direita, encontramos:
Como essa igualdade vale para todo e para todo , essas razões devem ser iguais a uma constante.
Vamos ter que resolver então as duas equações diferenciais:
Passo 2:
Agora vamos analisar 3 casos para os valores de :
Caso 1:
Se, então ele pode ser escrito da seguinte forma:
Assim:
A equação característica é:
E, portanto a solução vale:
Se você não se lembra disso, não se preocupe, basta revisar os capítulos anteriores.
Continuando na resolução do problema, observamos que não temos uma função trigonométrica, e, portanto esta função apenas será periódica de período 2 se . Como esta é a solução trivial, não pode ser negativo.
Caso 2:
Para
Assim,
Para que esta função seja periódica, deve ser igual a zero, e, portanto temos que , ou seja , é uma função constante. Lembra que falamos no início que função constante é válida como solução de
Agora vamos analisar na equação de . Com a equação ficará da seguinte forma:
Essa é uma equação de Euler ( não precisa ficar assustado rs). A solução dessa equação vale:
Gurde esse resultado. Daqui a pouco vamos analisar novamente para o caso em que
Caso 3:
Se , então ele pode ser escrito da forma: . Substituindo nas equações diferenciais:
A primeira equação é uma equação de Euler ( novamente, não se assustem!). A solução dessa equação é:
A equação de é mais tranquila não é mesmo? Já estamos acostumados a resolvê-la. Sua solução vale:
Porém deve ser periódica de período 2. E quando isso vai acontecer?
Devemos ter que . Para que isso aconteça é necessário que seja um inteiro positivo .
Passo 3:
Agora que já sabemos quais são as soluções para cada valor de , devemos analisar o que foi dito no problema. Observe que foi dito que está bem definida e é limitada para , ou seja, para todo, inclusive no infinito e portanto é limitada quando . Isso vai nos ajudar, e muito!
Primeiramente vamos analisar a equação de encontrada para λ=0:
Quando , então o termo tende a infinito. Porém, vimos que é limitada no infinito. Assim, obrigatoriamente, Como foi encontrado par que ela será constante para e também é uma constante, então as soluções fundamentais para , valem:
Agora vamos analisar a seguinte equação encontrada para λ>0:
Como é limitada, então também deve ser. Assim, como μ é um número inteiro positivo, quando o termo , o que não pode acontecer. Assim, obrigatoriamente, deve ser igual a zero. Já tínhamos encontrado as soluções de que vale:
Portanto, as soluções fundamentais valem:
Substituindo:
Passo 4:
Assumimos que pode ser escrita como uma combinação linear de soluções fundamentais. Assim:
Ufa, estamos quase chegando ao fim. Agora basta apenas determinar os coeficientes da série de Fourier. Para isso, vamos utilizar uma informação que é dada no problema:
Substituindo por, temos que:
De onde concluímos que: