Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Densidade de Células Unitárias: Volumétrica, Planar e Linear

Ver Todos os Exercícios

Teoria

Fala aí?! Bora aprender como calcular a densidade de células unitárias com o RespondeAí?!

Se liga nesse vídeozinho que o RespondeAí preparou especialmente pra você entender melhor sobre as densidades de células unitárias 👇

Ou se você preferir, continua comigo pra o nosso resumo em texto! 👇

Vamos aprender a calcular a densidade volumétrica, planar e linear! Mas você sabe porque que é importante estudar isso?!

Bem, essas densidades estão relacionadas a porosidade do nosso material, o que influencia nas propriedades mecânicas, elétricas e caloríficas do material!

Para calcular essas densidades a gente precisa entender o que é uma célula unitária e suas diferentes organizações, que são divididas em Cubo Simples (CS), Cubo de face centrada (CFS) e Cubo de Corpo centrado (CCC). Pra entender melhor essa divisão você pode clicar aqui!

Densidade Linear

A densidades atômica linear esta relacionado com as arestas dos cubos de face centrada e é dada pela seguinte fórmula:

  • é o comprimento linear que intercepta os círculos
  • é o comprimento linear dentro da célula, isso é, o comprimento da aresta da célula unitária.

Vamos resolver um exemplo pra ficar mais claro?!

Exemplo:

Vamos considerar a estrutura CCC (cúbica de corpo centrado) com direção .

  • Desenhamos a estrutura CCC:
Estrutura CCC.
Estrutura CCC.

  • Relacionamos o valor de e de :
  • Calculamos a densidade linear:

Densidade Planar

Algumas vezes, é importante determinar as densidades atômicas de alguns planos cristalográficos. Para calcularmos a densidade atômica planar usamos a seguinte fórmula:

éáá

A área que devemos usar é a do plano que intercepta a célula unitária, por exemplo: para o plano da célula unitária CCC. Nestes cálculos, para que a área de um átomo seja calculada, o plano considerado terá de interceptar o centro do átomo.

Exemplo:

Vamos calcular a densidade atômica planar (DAP) dos planos na rede cúbica de face centrada (CFC). Para isso vamos fazer um passo a passo!

  • Desenhar a estrutura CFC:
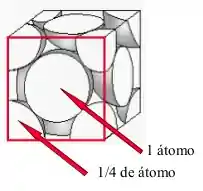
Estrutura CFC.
Estrutura CFC.
  • Calcular a área total de átomos:
    • Número de átomos: Temos de átomos nos cantos do cubo e um átomo inteiro no centro, isso nos dá um total de átomos
    • Área total de átomos:

Densidade Volumétrica

Podemos obter a densidade volumétrica de um metal a partir da célula unitária da estrutura cristalina e o valor do seu raio atômico usando da seguinte fórmula:

Onde:

  • é o número de átomos por célula unitária;
  • é a massa atômica
  • é o volume da célula unitária
  • é o número de avogadro igual a

As densidades variam conforme o tipo de material, a densidade dos metais é maior que dos cerâmicos que é maior que a dos materiais poliméricos.

âé

Esses materiais podem ser classificados da seguinte forma, segundo o Fator de empacotamento atômico (FEA):

  • Metais: Alto empacotamento (FEA), ligação metálica, elementos de elevada massa atômica
  • Cerâmicas: Baixo FEA, elementos leves
  • Polímeros: Baixo FEA ou amorfos, elementos leves .

Exercício:

Para um material hipotético com parâmetro de rede de . Determine a densidade planar de um plano para a célula CCC.

Confira a resolução no vídeo abaixo 👇👇👇

Agora vamos praticar com mais exercícios?!

Densidade Linear

Densidade Planar

Densidade Volumétrica

Exercício:

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Para um metal hipotético com parâmetro de rede de 0,31 nm. Determine a densidade planar de um plano (110) para a célula CCC

Passo 1

Primeiramente vamos definir a fórmula a ser aplicada:

DP = N° de átomos do plano / área do plano

Passo 2

Vamos determinar a área do plano:

A = B x h

A = a 2 × a

A = 0,31   n m 2 × 0,31   n m

A= 0,136 nm²

Passo 3

Determinando o número de átomos:

O plano intercepta o centro de 2 átomos (4 x ¼) + 1 = 2 átomos

DP = 2/ 0,136

DP= 14,70 átomos/ nm²

Resposta

DP= 14,70 átomos/ nm²

Exercício Resolvido #2

Elaboração própria

Para um metal hipotético com parâmetro de rede de 0,31 nm. Determine a densidade planar de um plano (010) para a célula CFC.

Passo 1

Primeiramente vamos definir a fórmula a ser aplicada:

DP = N° de átomos do plano / área do plano

Passo 2

Vamos determinar a área do plano:

A = B x h

A = a × a

A = 0,31 × 0,31

A= 0,0961 nm²

Passo 3

Determinando o número de átomos:

O plano intercepta o centro de 2 átomos (4 x ¼) + 1 = 2 átomos

DP = 2/ 0,0961

DP= 20,81 átomos/ nm²

Resposta

DP= 20,81 átomos/ nm

Exercício Resolvido #3

Elaboração própria

Determine a densidade linear na direção [110] da rede cristalina do cobre, cujo parâmetro de rede é 0,43 nm.

Passo 1

Primeiramente vamos definir a fórmula a ser aplicada:

D L = L c L I  

Passo 2

Vamos determinar o comprimento linear dentro da célula unitária ( L I )

Utilizando Pitágoras, teremos:

L c   ( x ) = a 2 + a ²

L c   x = 2 a 2  

L c   ( x ) = a 2

Como:

a = 0,43

L c   ( x ) = 0,43 2

L c   x = 0,6 1   n m

Passo 3

Comprimento linear que intercepta os círculos ( L c )

L c :     1   á t o m o   +   0,5   á t o m o   +   0,5   á t o m o =   2   á t o m o s  

Jogando na fórmula:

D L = L c L I = 2 0,6 1 = 3 , 28   á t o m o s / n m

Resposta

D L =     3,2 8   á t o m o s   / n m

Exercício Resolvido #4

Elaboração própria

Determine a densidade linear do alumínio CCC na direção [110} com parâmetro de rede de 0,51 nm.

Passo 1

Primeiramente vamos definir a fórmula a ser aplicada:

DL= Lc/LI

Passo 2

Pequenos grupos de átomos que se repetem, ou seja, a rede cristalina se subdivide em planos. Vamos determinar o comprimento linear dentro da célula unitária (LI)

DL = 1 átomo = 1 / (4² + 4²)1/2 = 1/5,657 = 0,177 * 108 átomos por A DL = 1,77 * 107 átomos/cm

L c   ( x ) = a 2 + a ² (Pitágoras)

L c   x = 2 a 2  

L c   ( x ) = a 2

L c   ( x ) = 0,51 2

L c   ( x ) = 0,721

Passo 3

Comprimento linear que intercepta os círculos (Lc)

Lc: 2 átomos

DL=2 / 0,721 = 2,77 átomos /nm²

Resposta

DL=2,77 átomos /nm²

Exercício Resolvido #5

Elaboração própria

Determine a densidade teórica do chumbo CFC que apresenta um parâmetro de rede de 0,495 nm e massa atômica de 207,2 g/g.mol

Passo 1

Primeiramente vamos definir a fórmula a ser aplicada:

ρ = n A V c N a

Onde:

n= número de átomos/cel. Unitária

A= massa atômica

Vc = volume da célula unitária

NA= número de Avogadro 6,02 x 10 23

Passo 2

V c = a ³

V c = ( 0,495 ) ³

V c = 0,121   n m 3 / c é l u l a

Passo 3

Cálculo da densidade.

ρ = n A V c N a

ρ = 4 × 207,2   0,121 × 6,02 × 10 ² ³

ρ = 1,1378 × 10 - 2 0 g / n m ³

Convertendo pra m³:

ρ = 1,1378 × 10 - 20 g n m ³ × ( 1   n m ) ³ ( 10 - 9 m ) ³

ρ = 1,1378 × 10 - 11 g m ³

Resposta

ρ = 1,1378 × 10 - 20

Exercício Resolvido #6

Elaboração própria

Quantas células unitárias estão presentes em 1   c m 3 do alumínio - C F C ? Sabendo que o raio atômico do alumínio é:

r A l = 0,1430   ∙ 10 - 7   c m

Passo 1

Primeiramente vamos definir como calcular o volume da célula unitária. Para o cálculo do volume temos:

V = a 3

Sendo “a” o parâmetro de rede, para C F C , temos:

a 2 = 4 r

  a = 4 r 2

Passo 2

Determinando o volume:

V = 4 r 2 3

V = 4 ∙   0,1430   ∙ 10 - 7   2 3

V = 64 ∙   0,002924207   ∙ 10 - 21   2 2

V ≅ 6,62   ∙ 10 - 23   c m 3

Passo 3

Pra gente fechar a questão e determinar a quantidade de células unitárias, basta a gente ver quantas vezes o volume de uma célula:

V ≅ 6,62   ∙ 10 - 23   c m 3

Cabe dentro do volume de 1   c m ³ de alumínio! Partiu:

X ∙ V = 1   c m 3

X = 1 V = 1   c m ³ 6,62   ∙ 10 - 23   c m ³

X = 1 V = 1   c m ³ 6,62   ∙ 10 - 23   c m ³

X ≅ 1,51   ∙ 10 22

Resposta

Aproximadamente 1,51   ∙ 10 22 células unitárias C F C cabem dentro de 1   c m 3 de alumínio

Exercício Resolvido #7

Elaboração própria

Se o raio atômico do chumbo (Pb) é de 0,175 nm , determine o volume da célula unitária em m³, considere a estrutura cristalina CFC.

Passo 1

Primeiramente vamos definir como calcular o volume da célula unitária:

Para o cálculo do volume temos:

V =   a ³ Sendo “a” o parâmetro de rede, então temos:

  a = 2 R 2

Passo 2

Determinando o volume:

V = 2 R 2 ³

V = 2 × 0,175 × 10 - 9 ³

Resposta

V = 12,13 × 10 - 29 m³

Exercício Resolvido #8

Elaboração própria

Calcule o raio de um átomo de ouro, que apresenta uma estrutura cristalina C C C e massa especifica de 19 ,   32 g c m 3 e um peso atômico de 196,96 g m o l .

Passo 1

Primeiramente vamos definir como calcular o volume da célula unitária. Para o cálculo do volume temos:

V =   a ³

Sendo “a” o parâmetro de rede, onde temos:

Por Pitágoras, do triângulo retângulo no interior do cubo, tiramos

a 2 2 + a 2 = 4 r 2

2 ∙ a 2 + a 2 = 4 2 ∙ r 2

3 ∙ a 2 = 4 2 ∙ r 2

a 2 = 4 2 ∙ r 2 3

a 2 3 2 = 4 2 ∙ r 2 3 3 2

a 2 ∙ 3 2 = 4 2 ∙ 3 2 ∙ r 2 ∙ 3 2 3 3 2

a 3 = 4 3 ∙ r 3 3 3

V = 64 ∙ r 3 3 3

Passo 2

Para determinarmos o raio temos de utilizar a fórmula da densidade teórica:

ρ = n A V C N a

Onde:

  • n = número de átomos= 2
  • A = massa atômica = 196 ,   96 g m o l
  • V C = volume da célula unitária = 64 ∙ r 3 3 3
  • N a = número de Avogadro 6,02   ∙   10 23

Achando R:

ρ = n ∙ A 64 ∙ r 3 3 3 ∙ N a

ρ = n ∙ A ∙ 3 3 64 ∙ r 3 ∙ N a

64 ∙ r 3 ∙ N a ∙ ρ = n ∙ A ∙ 3 3

r 3 = n ∙ A ∙ 3 3 64 ∙ N a ∙ ρ

r = n ∙ A ∙ 3 3 64 ∙ N a ∙ ρ 1 3

Substituindo:

r = 2 ∙ 196,96 ∙ 3 3 64 ∙ 6,02   ∙   10 23 ∙ 19,32 1 3

r = 1,40 ∙ 10 - 8   c m

Resposta

r = 1,40 ∙ 10 - 8   c m

Exercícios de Livros Relacionados

Para um monocristal CCC, você esperaria que a energia de superfície para um plano (100) fosse maior ou menor que para um plano (110)? Por quê? (Nota: Se necessário, consulte a solução para o Problema
A concentração de carbono em uma liga ferro-carbono é de 0,15%p. Qual é a concentração em quilogramas de carbono por metro cúbico da liga?
Determine o número do tamanho do grão ASTM se são medidos 20 grãos por polegada quadrada sob uma ampliação de 50 × .
O germânio forma uma solução sólida substitucional com silício. Calcule o número de átomos de germânio por centímetro cúbico para uma liga de germânio-silício que contém 15%p Ge e 85%p Si. As massas e
Para uma solução sólida formada por dois elementos (designados por 1 e 2), algumas vezes é desejável determinar o número de átomos por centímetro cúbico de um elemento em uma solução sólida, N 1 , dad