Determine no circuito abaixo, quando:
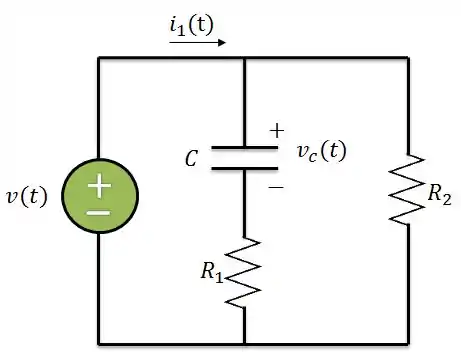
Passo 1
O enunciado nos pede a tensão no capacitor e a corrente quando a tensão da fonte é primeiro um degrau unitário e depois um impulso unitário . Vamos começar encontrando as equações de
Passo 2
Vamos aplicar a LCK e dividir a corrente que chega ao nó:
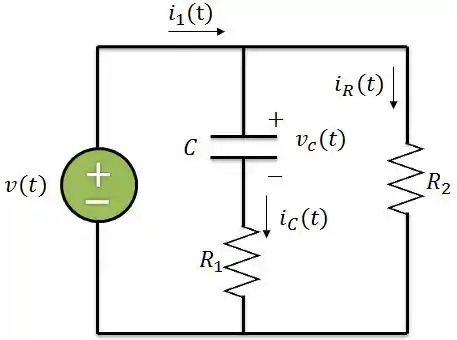
Passo 3
Aplicando a LTK no circuito, temos:
Como,
Substituindo:
Encontramos a EDO para a tensão no capacitor:
Passo 4
Na letra , . Ou seja, a tensão é zero até e para a tensão é constante igual a um.
Logo, para temos a seguinte EDO não homogênea:
Chegamos a uma EDO não homogênea. A solução geral dessa equação é composta pela solução particular mais a solução da homogênea.
Primeiro, vamos resolver a homogênea:
Para resolver essa equação, primeiro vamos obter a equação característica:
Logo a solução geral da equação é dada por:
sendo uma constante.
Passo 5
Agora, precisamos encontrar a solução particular.
Como é uma constante, a solução particular deve ser também uma constante:
sendo B uma constante.
Substituindo, temos:
Como a derivada de uma constante é zero:
Portanto, a solução geral é:
Passo 6
Agora, precisamos encontrar o valor da constante
O capacitor está inicialmente descarregado. Logo, para . Lembrando que a tensão no capacitor não pode variar instantaneamente, então:
Portanto, de acordo com a nossa condição inicial, temos:
Substituindo:
Logo, a tensão no capacitor para qualquer instante de tempo será:
Outra maneira de escrever seria:
Passo 7
Já encontramos para quando a fonte de tensão é um degrau unitário. Precisamos calcular agora.
A gente já tinha visto que:
Logo,
Acabamos de calcular o valor de e sabemos que .
Logo, para temos:
Logo,
Passo 8
Ufa! Terminamos a letra , vamos partir para Agora, . Já vimos que para o circuito:
Como, para o impulso unitário é zero:
Nós já resolvemos essa EDO na letra e vimos que resposta é:
Passo 9
Agora, vamos encontrar a constante . Como o impulso de tensão não pode ser aplicado no capacitor, ele deve ser aplicado no resistor , gerando um impulso de corrente de .
Como está em série com o capacitor. Esse impulso de corrente também passa pelo capacitor e de acordo com o teorema, um impulso de corrente de passando pelo capacitor faz com que sua tensão instantaneamente suba para .
Sabendo disso, já podemos calcular a constante .
Portanto, a resposta ao impulso unitário será:
Passo 10
Para terminar, precisamos encontrar para esse caso. A gente já tinha visto que:
Logo,
Acabamos de calcular o valor de e sabemos que .
Em , vimos que o impulso de tensão faz com que
Isso também ocorre com a corrente que passa pelo outro ramo:
Já para temos:
Portanto,
Que também podemos escrever assim: