Considere a cônica de equação
a) Efetue uma rotação de eixos que transforme o sistema no sistema de modo a obter uma equação sem o termo misto.
b) Identifique a cônica e faça um esboço do gráfico.
Passo 1
a) Pra começo de conversa, vamos escrever essa equação na sua forma matricial, igual a gente viu lá na teoria:
Vamos chamar a matriz de matriz . Precisamos encontrar os autovalores de , pra isso, precisamos fazer . Vamos lá pro próximo passo fazer isso.
Passo 2
Se , a gente quer dizer que:
Calculando esse determinante, vamos encontrar o polinômio característico:
Resolvendo essa equação do 2° grau, vamos encontrar os autovalores de :
Passo 3
Agora temos que encontrar os autovetores unitários de associados a cada autovalor.
O autovetor associado a será:
Sendo que .
Se , temos que
Multiplicando as matrizes, teremos esse sisteminha:
Da equação de baixo, tiramos que , então .
Arbitrando um valor qualquer para , por exemplo, , teremos que .
Mas nós queremos o autovetor unitário, então vamos dividir pela sua norma:
Boaa, finalmente encontramos o autovetor unitário de associado ao autovalor . Agora vamos encontrar o associado a .
Passo 4
O autovetor associado a será:
Onde .
Isso quer dizer que
O sistema encontrado vai ser
Da equação de cima temos que . Atribuindo , temos que:
Vamos novamente dividir pela norma para encontrar o vetor unitário:
Passo 5
Agora que temos os autovalores e autovetores, vamos reescrever a equação matricial, aquela que a gente fez lá no passo 1.
Reescrevendo ela com os autovalores e autovetores, ela fica assim
Fazendo a multiplicação de matrizes, vamos ter que
Se dividirmos os dois lados por 36, teremos
Que é a equação de uma elipse com focos no eixo , já que o denominador de é maior que o de :D
Passo 6
b) A equação dada no enunciado é a seguinte elipse
porém rotacionada.
Pra descobrir qual o ângulo de rotação dela, vamos analisar a matriz dos autovetores, afinal sabemos que
Então
Isso quer dizer que a elipse da equação foi rotacionada para obter a elipse do enunciado.
Pela equação , sabemos que e , então o gráfico da elipse é
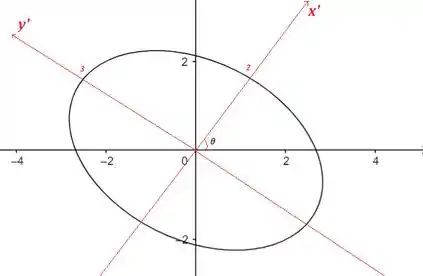
Resposta
a)
b) Elipse rotacionada.