Esboçar o gráfico da cônica de equação
Passo 1
O mesmo problema do anterior??

Exatamente!! Novamente, vamos esboçar a cônica dada pela expressão acima. Talvez, você ache um pouco chato, mas é fundamental fazermos vários exercícios para fixar bem o passo a passo.
Bora começar então!!
Passo 2
Como vimos na teoria, devemos começar montando a equação matricial da equação dada. Para isso, vamos primeiro retirar os valores das contantes e .
Da equação temos:
Vamos então colocar esses valores na equação matricial:
Nossa equação ficará:
Agora que temos nossa equação matricial conseguimos achar nossa matriz , que é:
Próximo passo é calcular os autovalores e autovetores dessa matriz!!
Passo 3
Bora calcular os autovalores da matriz .
Sempre usando a relação
Resolvendo o determinante:
Temos os valores:
Passo 4
Já temos os autovalores!! Agora, é encontrarmos os autovetores para cada autovalor.
Para , vamos supor que o autovetor é e devemos respeitar que:
Escolhendo uma das linhas, escolherei a primeira, mas sem um motivo especial:
Poderíamos ter escolhiso a segunda linha, o resultado final é o mesmo!!
Então, sabendo a relação e chutando , temos . Assim, nosso autovetor é:
Mas, ele não é unitário. Falta dividirmos por sua norma que é
Então untário é:
Agora, vamos calcular o autovetor para
Escolhendo uma das linhas, escolherei a primeira, mas sem um motivo especial:
Então, sabendo a relação e chutando , temos . Assim, nosso autovetor é:
Mas, ele não é unitário. Falta divifirmos por sua norma que é
Então untário é:
Passo 5
Agora que temos os autovalores e os autovetores podemos montar as matrizes e .
Montando :
Como foi montada de forma que a primeira linha é o autovalor , então a primeira coluna da matriz deve ser o autovetor relacionado ao autovalor , ou seja, .
Já temos tudo o que precisamos para montar nossa expressão matricial final:
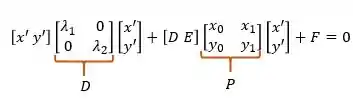
CUIDADO: na expressão acima quando temos [D E], o se refere ao valor que encontramos lá no início do exercício e não a matriz .
Montando com nossos valores teremos:
Fazendo a distributiva, temos:
Rearranjando para ficar na forma um pouco mais parecida com a forma canônica da parábola:
Chegamos na expressão de uma parábola. Sendo que a relação entre e é:
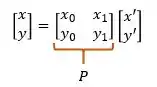
Teremos:
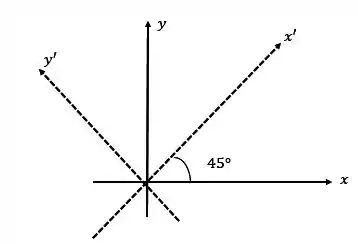
Como queremos um esboço, vamos analisar primeiro a matriz que nos dá o quanto o eixo girou. Como sabemos que:
Temos que:
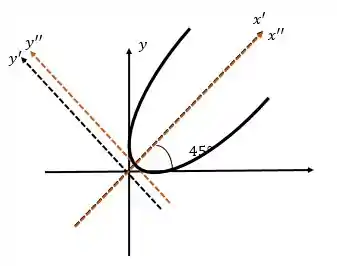
Então, nosso eixo estará da seguinte forma:
Além disso, nossa parábola possui uma translação em relação ao eixo , tal que:
Vamos achar o centro de . Para isso, sabemos que o centro de é
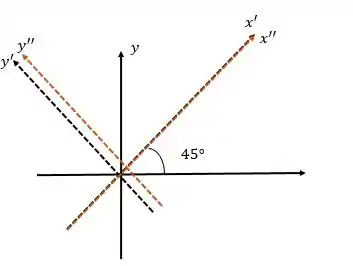
Para esboçar temos que lembrar da teoria do tópico 1 que vimos dois casos principais para a parábola, quando ela estava no eixo ou no eixo . A expressão que obtemos da parábola indica que estamos no CASO 2 da nossa teoria de parábolas.
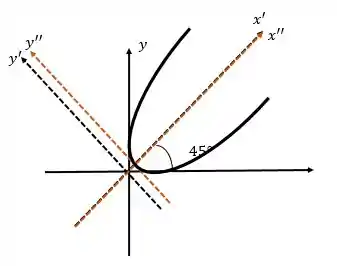
Realmente, plotando com um software, obtemos:
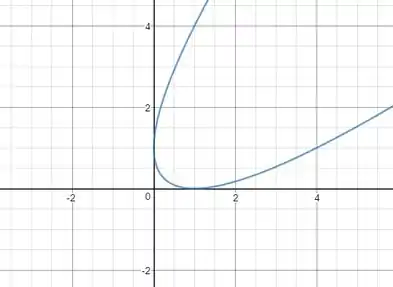
As contas nessa foram mais tranquilas!! Hehe

Resposta