Seja o lugar geométrica dos pontos do plano cujas coordenadas e satisfazem
- Identificar a cônica
- Encontrar as mudanças consecutivas das coordenadas que levam à forma canônica
- Encontrar a excentricidade de . Encontrar também as coordenadas dos focos e dos vértices, e as equações das assíntotas no sistema (se aplicável). Fazer um esboço do gráfico de .
Passo 1
Até agora estávamos esboçando as cônicas!! Nisso já estamos craques!! Hehe... Mas, vamos começar a complicar um pouco mais. Além de fazer tudo o que já fazíamos vamos começar a encontrar não só as cônicas, mas também seus parâmetros.
Passo 2
a) Nesse primeiro item devemos identificar a cônica, ou seja, fazer o que já vínhamos fazendo!
Como vimos na teoria, devemos começar montando a equação matricial da equação dada. Para isso, vamos primeiro retirar os valores das contantes e .
Da equação temos:
Vamos então colocar esses valores na equação matricial:
Nossa equação ficará:
Agora que temos nossa equação matricial conseguimos achar nossa matriz , que é:
Próximo passo é calcular os autovalores e autovetores dessa matriz!!
Bora calcular os autovalores da matriz .
Sempre usando a relação
Resolvendo o determinante:
Temos os autovalores:
Já temos os autovalores!! Agora, é encontrarmos os autovetores para cada autovalor.
Para , vamos supor que o autovetor é e devemos respeitar que:
Escolhendo uma das linhas, escolherei a primeira, mas sem um motivo especial:
Poderíamos ter escolhido a segunda linha, o resultado final é o mesmo!!
Então, sabendo a relação e chutando , temos . Assim, nosso autovetor é:
Mas, ele não é unitário. Falta dividirmos por sua norma que é .
Então untário é:
Agora, vamos calcular o autovetor para
Escolhendo uma das linhas, escolherei a primeira, mas sem um motivo especial:
Então, sabendo a relação e chutando , temos . Assim, nosso autovetor é:
Mas, ele não é unitário. Falta dividirmos por sua norma que é
Então untário é:
Agora que temos os autovalores e os autovetores podemos montar as matrizes e .
Montando :
Como foi montada de forma que a primeira linha é o autovalor , então a primeira coluna da matriz deve ser o autovetor relacionado ao autovalor , ou seja, .
Já temos tudo o que precisamos para montar nossa expressão matricial final:
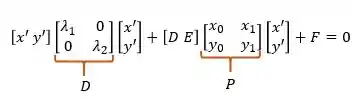
CUIDADO: na expressão acima quando temos [D E], o se refere ao valor que encontramos lá no início do exercício e não a matriz .
Montando com nossos valores teremos:
Fazendo a distributiva, temos:
Completando quadrados:
Dividindo tudo por :
Multiplicando tudo por
Chegamos na forma quase canônica da hipérbole. Para ficarmos na forma canônica faremos mais uma mudança de variável, considerando:
Teremos então:
Agora sim temos a expressão canônica da hipérbole. Esse item terminamos.
Passo 3
b) Agora precisamos determinar as mudanças consecutivas de coordenadas que fizemos para chegar na expressão canônica da hipérbole.
Bom, primeiro, mudamos das coordenadas para . A relação entre esses dois sistemas é dado por:
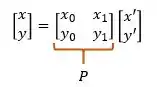
Então, substituindo nossa matriz , temos:
Teremos, então as relações:
Além dessa transformação fizemos uma translação do sistema para . No qual temos as relações:
Pronto!! São essas relações que o enunciado pede. Bora para o próximo item!!
Passo 4
c) Encontrar a excentricidade de . Encontrar também as coordenadas dos focos e dos vértices, e as equações das assíntotas no sistema (se aplicável). Fazer um esboço do gráfico de .
Esse item já fizemos várias vezes quando falamos de cônicas!! O que muda agora, é que antes tínhamos no máximo uma translação, ou seja, uma mudança de variáveis, e agora, temos duas mudanças. Mas, isso não altera a forma de resolução. Ou seja, vamos achar todas as variáveis no sistema em que a curva está no sistema canônico e depois por meio das relações que achamos no item anterior passamos para o sistema .
Então, considerando a equação:
Estamos no CASO 1 da hipérbole. Assim, sabemos que:
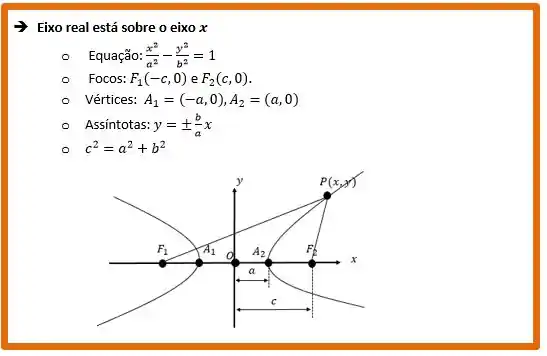
Olhando para nossa expressão e as relações acima, temos:
Usando a relação
Lebrando que todos os parâmetros que encontraremos estarão no sistema .
Teremos:
Encontramos tudo o que percisávamos no sistema , agora vamos passar para o sistema e depois para o sistema . Para a primeira mudança, usaremos:
Usando as relações acima obteremos os parâmetros em :
A excentricidade não muda, pois só depende de e .
Para chegarmos na nossa solução vamos passar do para , usando:
Fazendo as contas, teremos:
Para passar as assíntotas para teremos que primeiro isolar nas nossas relações acima e . Isolando teremos:
Substituindo:
Estamos quase terminando, falta o esboço, que fica mais ou menos:
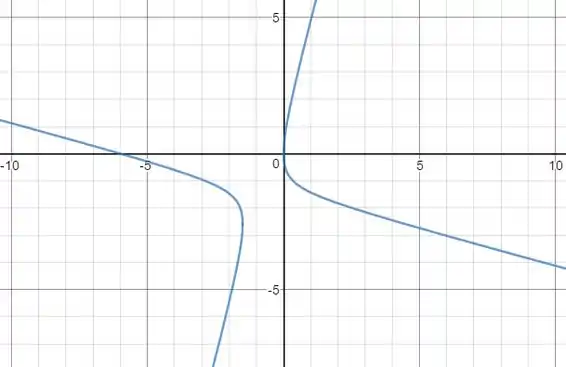
Ufa!! Cansei!! Esse tipo de exercício requer muita atenção por causa das contas que são muito fáceis de errar. Então, faça com calma e para pegar agilidade nada como fazer vários exercícios!
