Mostre porque um contralador do tipo PI anula o erro em regime estacionário para um processo de ordem e uma entrada do tipo degrau unitário no distúrbio.
Passo 1
Vamos tentar esboçar um diagrama de blocos genérico para a situação acima:
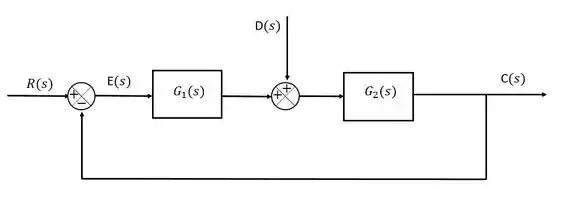
Nesse caso, é a variável controlada, é a referência (setpoint), o distúrbio.
A função de transferência é a função de transferência do controlador proporcional integral:
E a função de trsnferência é um processo qualquer de ordem . Vamos continuar nos referinda a ela como somente .
Passo 2
Sendo assim vamos tentar calcular a expressão para o erro nesse sistema e em seguida calcular o erro em regime permanente utilizando o teorema do valor final.
Pelo diagrama de blocos temos:
Substituindo a segunda na primeira:
Por fim:
Passo 3
Agora que já temos a expressão do erro podemos começar a substituir as nossas funções.
Como a variação foi no distúrbio e não no setpoint, temos que:
Portanto:
Como é o nosso PI:
Então:
Passo 4
Aplicando o teorema do valor final:
Logo:
Multiplicando em cima e embaixo por :
Dessa forma, se a função for do tipo , o erro então também será visto que o termo que tende a zero no denominador não vai poder ser simplificado. Então, aplicando o limite:
Resposta
Ei, a resposta está no passo a passo :)