Considere a reta definida por
Seja a tranformação linear que é a reflexão com relação a reta
- Determine
- Seja onde é o plano que contém e é ortogonal à reta Determine
- Determine os autovalores de e os autoespaços associados de cada autovalor.
- Determine uma base de tal que seja diagonal.
- é ortogonalmente diagonalizável? Se sua resposta foi afirmativa, diagonalize ortogonalmente. Se sua resposta foi negativa, justifique.
- Determine
- Determine uma base de
- Determine explicitamente as matrizes e onde é a matriz de na base canônica.
Passo 1
(a) Queremos a reflexão do vetor pela reta gerada por ele mesmo!
Mas nesses casos, quando o vetor pertence a reta da reflexão, o resultado vai ser o próprio vetor!
Assim:
Passo 2
(b)A situação que temos é a seguinte:
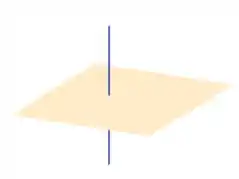
Sabendo que o plano contém a origem e a reta também, esse ponto de interseção vai ser a própria origem.
Como está nesse plano, ele vai ser ortogonal a reta em que estamos refletindo. Nesses casos,
Passo 3
(c) Como é uma reflexão por uma reta seus autovalores vão ser 1 e .
O autoespaço associado ao autovalor 1 vai ser a própria reta pois assim como vimos na letra (a), as reflexões dos vetores pertencentes a reta em que estamos refletindo vão ser os próprios vetores.
Já o autoespaço associado ao autovalor vai ser o plano da letra (b) por ser o complemento ortogonal da nossa reta. Ou seja, por conter todos os vetores ortogonais a reta!
A reflexão de um vetor ortogonal ao espaço em que estamos refletindo vai ser o próprio vetor com sentido invertido (mesmo módulo e direção), por isso atribuímos esse autovalor.
Vamos então, achar
Sei que é ortogonal ao plano e ele contém a origem, assim, sua equação cartesiana vai ser:
Passo 4
(d) Basta que seja a união de uma base de com uma base de , ou seja, .
Temos a base de
A base de podemos tirar da equação cartesiana :
Assim,
Passo 5
(e) Para isso, precisamos achar uma base ortonormal de formada de autovetores de . Eu já tenho, para transformar isso em ortogonal, vou substituir o terceiro vetor por um ortogonal aos dois primeiros que vou achar fazendo produto vetorial:
Então temos uma base ortogonal do composta de autovetores de : ,
Se acharmos uma base ortonormal vai ficar mais fácil de invertermos na diagonalização! Pois quando temos uma base ortonormal nas colunas, .
Vamos fazer isso então, apenas normalizando os vetores de
Assim,
Passo 6
(f) Como não é autovalor de , a dimensão do autoespaço associado a ele, ou seja, o núcleo, vai ser 0!
Passo 7
(g) Antes de pensar em achar a imagem, bora testar uma coisa: vamos usar o TNI para achar a dimensão da imagem:
Como a imagem pertence ao e sua dimensão é 3, ela vai ser o próprio
Podemos, então, pegar qualquer base do para ser base da imagem, como a canônica:
Passo 8
(h) Como é uma matriz reflexão, se eu aplicá-la um número ímpar de vezes, vai resultar a primeira reflexão, ou seja, vai ser como se eu tivesse aplicado a matriz uma vez só. Assim,.
Agora, se eu refletir (aplicando 1 vez) e depois refletir novamente, acabo voltando ao vetor inicial (aplicando 2 vezes) e isso não acontece apenas quando aplico 2 vezes, mas sempre que aplico um número par de vezes! Assim, .
Passo 9
Vamos encontrar para isso, é só multiplicar que encontramos na letra e):
Assim, e
Resposta
(a)
(b)
(c) e é o plano
(d)
(e)
(f)
(g)
(h) e